Примеры некоторых конфигураций

Электрических полей

а) Однородное поле

Если в некоторой области пространства вектор напряженности электрического поля остается постоянным, т. е. имеет неизменное направление и абсолютную величину, то говорят, что в этой области пространства электрическое поле однородно. В однородном поле связь между напряженностью поля и потенциалом упрощается, приобретая, как следует из (3), вид

Рис. 1 , (4)

где — разность потенциалов между любыми двумя эквипотенци-альными плоскостями, а — расстояние между ними.

Примером однородного электрического поля служит поле внутри плоского конденсатора (т. е. между двумя близко расположенными параллельными проводящими пластинами, несу­щими равные по модулю, разноименные заряды). Сказанное иллюстрирует рис. 1.

б) Поле диполя

Точечный электрический диполь — это система 2-х одинаковых по величине, но разных по знаку, точечных зарядов, расстояние l между которыми значительно меньше расстояния от зарядов до точки наблюдения, где определяется поле системы. Вектор проводится от отрицательного к положительному заряду (см. рис. 2). Так же ориентирован и электрический дипольный момент, который, по определению, равен . Чтобы составить представ-ление о конфигурации поля диполя, учтем, что картина силовых линий обладает осевой симметрией. Это позволяет ограничиться изображением поля в любой плоскости, содержащей вектор . Соответствующее изображение дано на рис. 3, содержащем силовые (сплошные) и эквипотенциальные (пунктир) линии.

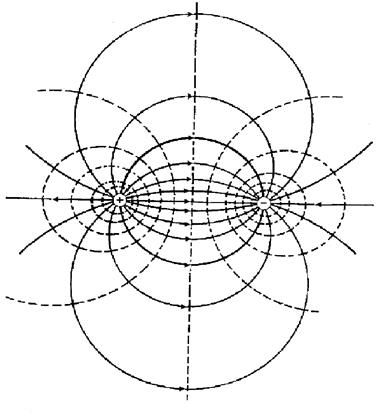
Рис. 3

Описание экспериментальной установки

Изучаемые электрические поля образуются с помощью металлических электродов. В каждом случае используется пара электродов различной формы (пластины, цилиндры и т. п.), между которыми поддерживается постоянное напряжение. Так называется разность их потенциалов.

Известно, что в электростатическом случае (когда поле постоянно, а токи отсутствуют) все точки проводника обладают одинаковым потенциалом. Так что внутри проводника электростатического поля нет, и анализ структуры поля связан с наружным пространством.

Особенностью предлагаемой лабораторной работы является то, что присущая электростатическим условиям структура полей изучается в ней в заведомо не электростатических, хотя и стационарных (поле постоянно, но есть постоянный ток) условиях. Причина возможности подобной подмены заключается в следующем. В физике вообще и в электродинамике, в частности, нередко случается, что уравнения для различных физических условий имеют в точности одинаковый вид. Используемые символы (буквы) в них могут, конечно, отличаться, но математическая форма уравнений совпадает. А у одинаковых уравнений — одинаковые решения! Именно это обстоятельство используется авторами этой лабораторной работы. Оказывается, что уравнения и граничные (между областями с разной проводимостью ) соотношения к ним, описывающие электрическое поле в условиях постоянного тока, обнаруживают формальную аналогию с уравнениями электростатического поля в диэлектриках, отличаясь от них лишь заменой диэлектрической проницаемости на . Это позволяет, изучая конфигурацию токов, фактически выявлять конфигурацию электростатического поля.

В данной лабораторной работе металлические электроды, о которых говорилось в начале раздела, разделены не диэлектрической, а проводящей средой. Роль последней играет электропроводящая пленка, к которой прижаты электроды. По пленке течет ток, причем распределение потенциала (а значит, и электрического поля) в ней совпадает с распределением электростатического потенциала (в отсутствие пленки), создаваемого электрически заряженными телами такой же конфигурации, что и электроды.

Схема лабораторной установки дана на рис. 4. На ней указаны основные элементы (обеспечивающие требуемый токовый режим и возможность измерения потенциала): источник постоянного тока, электроды, вольтметр, щуп, указана также ориентация декартовых осей.

Представленный на схеме (рис. 4) прямоугольник с электродами символизирует место, где располагают плату для моделирования полей. Всего таких плат четыре: 1) плоские электроды; 2) «сектор»; 3) диполь; 4) проводник переменного сечения. На рис. 5 эта область занимает нижнюю половину. Там же представлен так называемый пантограф (устройство для вычерчивания копий). Пантограф содержит горизонтальную рейку, которую можно перемещать в перпендикулярном направлении (по оси у) с отсчетом координаты у по «вертикальной» линейке и фиксировать. По рейке, в свою очередь, перемещают каретку с отсчетом координаты х по горизонтальной линейке. Каретка несет держатель щупа (внизу рис. 5) и упругий кронштейн с держателем фломастера (средняя часть рис. 5). При нажатии щуп касается металлическим электродом проводящей пленки, размещенной на плате. Подключенный к щупу вольтметр регистрирует потенциал соответствующей точки. Когда нужный потенциал найден, нажимают на упругий кронштейн, и фломастер отмечает положение этой точки на миллиметровке. Одновременно регистрируют декартовы координаты этой точки.

Порядок выполнения работы

1. В пазы каркаса вставьте плоские электроды (плата 1 для моделирования полей). Слегка прижмите плату винтом, выступающим вправо из борта каркаса.

2. Расположите лист миллиметровой бумаги на пластине конденсатора, наколов углы миллиметровки на шпильки.

3. Вставьте щуп и фломастер в их держатели.

4. Подвижную рейку, несущую щуп и фломастер, зафиксируйте винтом, при этом фиксируется и предварительно выбранное значение координаты y.

5. Перемещая по рейке мелкими шагами каретку, предварительно установленную в крайне левое положение, т.е. изменяя только координату x, измеряйте на каждом шаге по показаниям вольтметра значения потенциала с тем, чтобы найти координаты, соответствующие заранее выбранному его значению. Найденное положение нажатием (с небольшим усилием) на фломастер отмечайте на миллиметровке.

6. Передвигая подвижную рейку с шагом, равным 10 мм, по оси y вплоть до конца платы, повторите п. 5 для каждого шага.

7. Повторите пп. 1—6 для оставшихся трех других плат.

Представление результатов эксперимента

На миллиметровках с нанесенной системой точек построить эквипотенциальные линии (с указанием значений соответствующих потенциалов) и силовые линии электрического поля.

Контрольные вопросы

1. Цель работы.

2. Каким образом обнаруживается присутствие электрических полей?

3. Представление о точечном заряде. Сила его взаимодействия с электрическим полем.

4. Конфигурации полей и их наглядное представление. Силовые линии.

5. Потенциальность стационарных электрических полей.

6. Потенциал и его взаимосвязь с полем. Неоднозначность потенциала.

7. Представление об эквипотенциальных поверхностях и линиях. Взаимная ориентация силовых линий и эквипотенциальных поверхностей (линий).

8. Однородное поле. Его взаимосвязь с потенциалом.

9. Напряженность и потенциал поля точечного заряда. Закон Кулона. Потенциальная энергия взаимодействия двух точечных зарядов.

10. Определение электрического дипольного момента.

11. Характеристика метода исследования конфигурации поля, используемого в работе.

12. Содержание лабораторных упражнений. Порядок их выполнения.

Литература

1. А.В. Астахов, Ю.М. Широков. Курс физики. Т. 2. Электромагнитное поле. М.: «Наука», 1980. 359 с.

2. И.Е. Иродов. Электромагнетизм. Основные законы. М.-СПб.: Физматлит, 2000. 350 с.

3. С.М. Крейнин. Физические системы: модели, состояния, уравнения и законы движения. Т. 1. М.: Изд-во ООО «ИПЦ “Маска”», 2009. 476 с.

4. Д.В. Сивухин. Общий курс физики. Т. 3. Электричество. М.: «Наука», 1977. 688 с.

5. Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике. М.: «Мир», 1966. Вып. 5. 296 с.

Дата добавления: 2015-10-29