Стационарных электрических полей

Цель работы

Построение эквипотенциальных и силовых линий для различных электрических полей (однородного поля, поля диполя и др.).

Теоретическое введение

Электрическое поле считается полностью охарактеризованным, если в каждой точке пространства известен вектор электрической напряженности . Напряженность в точке с радиус-вектором — это «сила», которая действует на единичный положительный заряд, находящийся в этой точке. Силовой ли­нией электрического поля называется линия, касательная к которой в каждой ее точке совпадает по направлению с вектором . Силовые линии применяют для графического изображения электрических полей. Если в каждой точке напряженность остает­ся неизменной во времени, то электрическое поле называется стацио­нарным. Стационарное электрическое поле потенциально. Это означает, что работа по перемещению любого заряда в таком по­ле не зависит от траектории, по которой осуществляется это пере­мещение, а определяется только положениями начальной и конечной точек траектории. Поэтому стационарное электрическое поле можно описывать не только с помощью вектора напряженности, но и посредством скалярной величины — потенциала 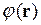. Потенциал в точке с радиус-вектором численно равен работе, которую требуется совершить, чтобы переместить единичный положительный заряд из бесконеч­ности в эту точку. (При этом предполагается, что поле создается ограниченной в пространстве системой зарядов и потенциал на бесконечности равен нулю). По сути дела, потенциал 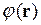— это потенциальная энергия, которой обладал бы единичный положительный за­ряд, если бы он оказался в точке . 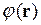Зная потенциал во всех точках поля, легко найти и напряженность поля. Онаравна градиенту потенциала, взятому с об­ратным знаком:

. (1)

Градиент скалярной функции в данной точке пространства есть вектор, декартовы компоненты которого суть частные производные этой функции (со знаком «») по соответствующим декартовым координатам, вычисленные в выбранной точке. То есть

(2)

Эквипотенциальной поверхностью в электрическом поле называется поверхность, все точки которой имеют одинаковое значение потенциала. Силовые линии электрического поля могут пересекать эквипотенциальные поверхности только под прямым углом. Рассмотрим скалярное произведение 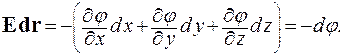Если вектор 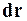лежит в плоскости, касательной к эквипотенциальной поверхности, то приращение потенциала равно нулю. Следовательно, электрическое поле перпендикулярно к эквипотенциальной поверхности. Простая формула

(3)

важна для расчета разности потенциалов.

Дата добавления: 2015-10-29