Лабораторная работа Э.6

ИЗУЧЕНИЕ ЯВЛЕНИЯ ВЗАИМНОЙ

ИНДУКЦИИ

Цели работы

1) Исследование взаимной индукции коаксиально расположенных соленоида и короткой катушки.

2) Определение значений взаимных индуктивностей.

Теоретическое введение

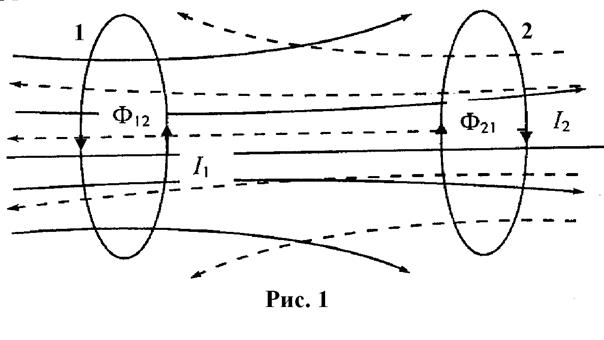
Рассмотрим два неподвижных контура 1 и 2, расположенных близко друг к другу (рис. 1). Если по контуру 1 течет постоянный ток I ₁, то в окружающем этот контур пространстве возникает магнитное поле, которое можно изобразить графически с помощью магнитных силовых линий (сплошные линии на рисунке). Часть этих линий пронизывает контур 2, создавая в нем магнитный поток . Здесь B ₁– магнитная индукция, создаваемая током I ₁ в области поверхности S ₂, натянутой на контур 2, по которой ведется интегрирование. Подынтегральное выражение является скалярным произведением векторов, указанных в скобках.

При этом вектор dS определяется так:ô dS ôравен площади dS элемента поверхности интегрирования, направление вектора dS задает единичный вектор нормали n к dS (ô n ô = 1), так что dS = n dS. Поэтому величина (B dS) = (Bn) dS = B _n dS, где B _n – проекция B на выбранную нормаль.

Аналогично, если по контуру 2 течет ток I ₂ (магнитное поле этого тока изображено пунктирными линиями на рис. 1), то магнитное поле этого тока создает в контуре 1 магнитный поток F₁₂.

Согласно закону Био-Савара магнитная индукция B ₁, создаваемая током I ₁, пропорциональна этому току, поэтому магнитный поток F₂₁ также (в отсутствие ферромагнетиков) пропорционален величине I ₁, т.е. выполняется равенство

F₂₁ = L ₂₁ I ₁. (1)

Понятно, что (в отсутствие ферромагнетиков) должно выполняться и симметричное равенство

F₁₂ = L ₁₂ I ₂. (2)

Коэффициенты пропорциональности L ₂₁ и L ₁₂, входящие в формулы (1) и (2), называются взаимными индуктивностями или коэффициентами взаимной индукции.

При изменении тока I ₁ в первом контуре, величина магнитного потока F₂₁, пронизывающего контур 2, также изменяется, поэтому в нем индуцируется ЭДС

. (3)

Соответственно имеет место и формула

. (4)

Взаимная индуктивность L ₁₂ зависит от формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости окружающей среды. Можно показать, что если взаимодействующие контуры находятся в среде, не имеющей ферромагнитных свойств, то выполняется так называемая теорема взаимности: L ₁₂= L ₂₁.

Рассмотрим теперь взаимодействие катушек с плотной намоткой проводников. В этом случае полный магнитный поток, пронизывающий катушку, равен сумме потоков, пронизывающих каждый ее виток, Величина Y называется также потокосцеплением.

Для потокосцеплений Y₁₂ и Y₂₁ справедливы выражения Y₁₂ = L ₁₂ I ₂ и Y₂₁ = L ₂₁ I ₁, аналогичные формулам (1) и (2), где теперь L ₁₂ и L ₂₁ – взаимные индуктивности катушек.

Если в обеих катушках протекают одновременно токи I ₁ и I ₂, то полное потокосцепление катушек Y состоит из суммы магнитных потоков Y₁₁ и Y₂₂ через каждую катушку, обусловленных их собственными магнитными полями, и магнитных потоков Y₁₂ и Y₂₁, возникающих вследствие магнитного взаимодействия катушек между собой:

Y = Y₁₁+Y₂₂ ± (Y₁₂+Y₂₁). (5)

Знак взаимного потокосцепления Y₁₂ в формуле (5) определяется взаимной ориентацией магнитного поля B ₁, создающего в катушке 1 собственный поток Y₁₁ имагнитного поля B ₂, создающего в ней же поток Y₁₂. Это же правило определяет знак величины Y₂₁. Если по катушкам протекает одинаковый ток, то величина полного потокосцепления пропорциональна силе этого тока:

Y = LI. (6)

В этом случае справедливо следующее равенство:

L = L ₁ + L ₂ ± 2 L ₁₂, (7)

где L ₁ и L ₂ – собственные индуктивности катушек и L ₁₂ их взаимная индуктивность.

В лабораторной работе определяется взаимная индуктивность длинной катушки 1 (соленоида) и короткой катушки 2, расположенной соосно с соленоидом, причем так, что ее центр смещен относительно одного из торцов на расстояние x (см. рис. 2).

Пусть N ₁ – число витков в соленоиде и N ₂ – число витков в короткой катушке, пусть далее B _c – магнитная индукция. создаваемая соленоидом, и S – площадь поперечного сечения короткой катушки. Известно, что магнитное поле, создаваемое внутри соленоида, является однородным, т.е. B _c» const, поэтому взаимное потокосцепление короткой катушки равно

Y_{21 =} N ₂ B _c S. (8)

Сопоставляя формулы Y₂₁ = L ₂₁ I ₁ и (8), находим

(9)

Величина магнитной индукции B _c на оси соленоида в произвольной точке А, находящейся на расстоянии x от его левого торца (см. рис. 2), дается следующим выражением (вывод этой формулы дан в приложении к работе Э.5):

, (10)

где

(11)

и – погонная (на единицу длины) плотность витков соленоида.

Из формул (10) и (11) видно, что в центре бесконечно длинного соленоида ()

= »1 и 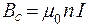. (10а)

Соответственно на краю соленоида (левом) =0, »1, в этом случае:

. (10б)

Таким образом, величина магнитной индукции в центре длинного соленоида в два раза больше, чем на краю.

Подставив формулы (10) и (11) в выражение (9), получим величину взаимной индукции L ₂₁ в зависимости от координаты x короткой катушки относительно левого края соленоида:

. (9a)

Дата добавления: 2015-10-29