Лабораторная работа Э.5

ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ

СОЛЕНОИДА

Цели работы

1) Определить индукцию магнитного поля внутри соленоида и катушки.

2) Сравнить экспериментальные результаты с расчетом.

Теоретическое введение

Магнитное поле порождается движущимися зарядами и оказывает силовое воздействие на движущиеся заряженные объекты. Упорядоченное движение зарядов называют электрическим током. Таким образом, во-первых, токи создают магнитное поле и, во-вторых, в свою очередь магнитное поле действует на токи. Если сила тока I не изменяется (постоянный ток), то магнитное поле, порожденное таким током, также не изменяется во времени и называется стационарным (в противном случае – переменным).

Одной из основных характеристик магнитного поля является вектор магнитной индукции В (Тл). Вектор В определяет величину и направление силы, с которой магнитное поле действует: а) на любой точечный заряд, движущийся со скоростью v в произвольной точке пространства, где есть магнитное поле:

– так называемая магнитная сила Лоренца;

б) на элемент длины dl линейногопроводника (достаточно малого поперечного сечения) с током I:

– сила Ампера.

Здесь вектор dl направлен вдоль провода в направлении тока, квадратными скобками обозначено векторное произведение заключенных в них сомножителей.

Закон Био – Cавара позволяет рассчитать величину и направление вектора индукции магнитного поля, созданного элементом тока в произвольной точке пространства на расстоянии r от тока:

Здесь = 4 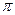∙10^-7 Гн/м – магнитная постоянная, – радиус-вектор, проведенный от элемента тока в точку наблюдения. Индукция магнитного поля , созданного всем током I может быть найдена суммированием полей , созданных в точке наблюдения всеми элементами этого тока. Такой способ расчета опирается на принцип суперпозиции: магнитное поле, создаваемое несколькими токами, равно векторной сумме магнитных полей, создаваемых каждым током в отдельности. Таким образом, полное поле в точке наблюдения есть

. (1)

Использование закона Био-Савара и принципа суперпозиции позволяет рассчитать значения индукции магнитного поля в любой точке на оси катушек, что является задачей эксперимента. Лабораторная аппаратура позволяет измерить величину индукции поля катушек в определенных точках и сравнить расчетные данные с экспериментальными.

В приложении показано, что величина индукции поля на оси катушки в произвольной точке с координатой x, отсчитываемой от (центр катушки), дается выражением

(2)

Здесь N – число витков катушки, l – ее длина, x – координата точки наблюдения на оси катушки, R – радиус катушки, и – углы между осью катушки и лучами из точки x к краям катушки (рис. 1).

Примерная картина структуры и величины магнитного поля внутри короткой и длинной катушек приведена на рис. 1.

Если выполняется соотношение 2R l (длинную катушку называют соленоидом), то в точке с координатой (торец) имеют место равенства α₁= и α₂ , а в центре соленоида (x= 0) — α₁ и α₂ . В этом случае расчет величины магнитной индукции на оси соленоида в центре В _ци в торце В _тпо формуле (2) дает

(3)

Дата добавления: 2015-10-29