Диэлектрической проницаемости

Экспериментальные измерения физических характеристик не всегда являются прямыми, т. е. непосредственно считываемыми с показаний приборов. Чаще производится непосредственное измерение иных величин, которые, однако, связаны с искомыми надежно установленными закономерностями. Так что на последнем этапе ис-следуемая характеристика определяется в результате вычисления по формулам, выражающим указанные закономерности. Процедуру подобного опосредственного определения представляющих интерес физических величин, основанного на экспериментальном исследовании, именуют косвеннымизмерением. Данная работа имеет дело именно с такого рода измерениями.

Цели работы

1) Теоретический расчет и измерение (двумя с пособами) электроемкости воздушного конденсатора.

2) Измерение диэлектрических проницаемостей образцов веществ, поочередно располагаемых между пластинами конденсатора.

Теоретическое введение

Диэлектрики (изоляторы) — это вещества, не проводящие электрического тока: их заряды, входящие в состав молекул или ионов, не способны далеко перемещаться. Будучи внесенным во внешнее электрическое поле диэлектрик поляризуется. Явление поляризации независимо от ее механизма (различного у полярных и неполярных молекул и диэлектрических кристаллов) заключается в смещении всех положительных зарядов по направлению поля, а отрицательных зарядов — в прямо противоположном направлении.

Количественное описание явления поляризации опирается на представление о дипольной системе зарядов. Электрический диполь — этосистема из двух разноименных точечных зарядов, одинаковых по модулю 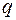и разделенных расстоянием (плечом диполя) l. Электрическим дипольным моментом этой системы называют вектор 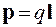, направленный от отрицательного заряда к положительному.

Поляризованный диэлектрик характеризуют вектором P, именуемым поляризованностью (или просто поляризацией), который равен дипольному моменту единицы объема. Если поляризующее поле не слишком велико, то поляризованность Р пропорциональна внешнему полю Е, т. е. P= e₀ c E. Здесь e₀ — электрическая постоянная. Безразмерный коэффициент 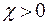называется диэлектрической восприимчивостью.

Основной физической характеристикой диэлектрика служит e — диэлектрическая проницаемость вещества, равная 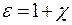. Для всех веществ 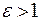, для вакуума 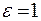. Диэлектрическая проницаемость показывает, во сколько раз поле (или сила кулоновского взаимодействия между зарядами) в диэлектрической среде слабее, чем в вакууме.

Диэлектрическую проницаемостьвеществудобноизмерять, используя конденсатор. Последнийпредставляет собой систему двух близко расположенных проводников (так называемых обкладок). Поле, создаваемое таким устройством в заряженном состоянии, практически полностью сосредоточено в пространстве между обкладками. Это значит, что силовые линии вектора Е, начинающиеся на одной обкладке, заканчиваются на другой, т. е.заряды на обкладках должны быть одинаковыми по модулю и противоположными по знаку. Основной характеристикой конденсатора является емкость 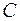. Последняя определяется формулой

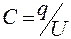, (1)

где U — разность потенциалов между обкладками (называемая также напряжением). B CИ за единицу электроемкости принят фарад (Ф). Емкостью в 1 Ф обладает конденсатор, у которого заряд в 1 Кл создает между обкладками напряжение в 1 В. Фарад — чрезвычайно большая единица емкости. Он соответствует емкости уединенного проводящего шара радиусом в 9 млн км, что в 1400 раз превышает радиус Земли. Поэтому емкости используемых на практике конденсаторов измеряются в микрофарадах и пикофарадах (1мкФ=10^-6 Ф, 1пФ=10^-12 Ф).

Конденсаторы могут иметь различную геометрическую форму. Существуют, например, сферические, цилиндрические и плоские конденсаторы. В данной лабораторной работе экспериментальные измерения связаны с использованием плоскогоконденсатора (будем называть его измерительным). Плоский конденсатор — устройство, состоящее из двух параллельных плоских проводящих пластин, расстояние между которыми мало по сравнению с линейными размерами пластин. Если объем между пластинами ничем, кроме воздуха, не заполнен, то устройство называется воздушным конденсатором. Его емкость равна

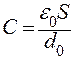. (2)

Здесь S — площадь пластины, 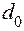— расстояние между пластинами. Если же объем конденсатора заполнен диэлектриком, то его емкость есть

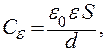(3)

где теперь расстояние между пластинами конденсатора определяется толщиной d твердой диэлектрической пластины, диэлектрическая проницаемость которой .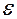

Схема эксперимента.

Работа строится на использовании схем, представленных на рисунках 1 и 2. Здесь С — измерительныйконденсатор, R ₀ — эталонное сопротивление, C ₀ — эталонный конденсатор, U и U ₀ — напряжения на измери-

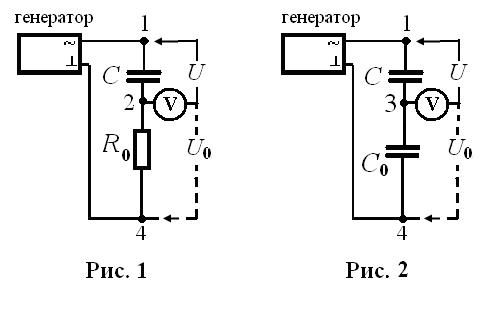
тельном конденсаторе и эталонных элементах R ₀и C ₀ соответственно. Клеммы 1, 2 (рис.1) и 1, 3 (рис.2) служат для поочередного подключения вольтметра к С и R ₀ (рис.1) или С ₀ (рис.2). В схеме используется генератор переменного тока частоты .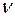

Особая роль в этой лабораторной работе отводится измерительному плоскому конденсатору С. В первом упражнении, когда конденсатор С является воздушным, а расстояние между его пластинами равно d ₀, определяется емкость этого конденсатора, причем как в результате теоретического расчета, так и экспериментально (двумя способами).

Во втором упражнении это же устройство заполняют поочередно диэлектрическими пластинами различной толщины 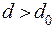( 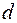— это и новое расстояние между обкладками), определяют соответствующие значения емкости 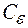и диэлектрической проницаемости :

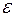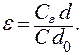(4)

Числовые значения постоянных величин d ₀, R ₀, C ₀ и 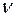, входящих в расчетные формулы, даны в таблице 1.

d 0	R 0	С 0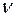
1,8 мм	2,01 кОм	9,3 нФ	2,0 кГц

Таблица 1

Упражнение I

Дата добавления: 2015-10-29