Linear/ Nonlinear System Solving Solve Blocks

The general form for using system solving functions in Mathcad is within the body of a solve block. There are four general steps to creating a solve block. These are:

1. Provide an initial guess (definition) for each of the unknowns you intend to solve for. Mathcad solves equations by making iterative calculations that ultimately converge on a valid solution. The initial guesses you provide give Mathcad a place to start searching for solutions. Guess values are usually required for all systems.

2. Type the word Given in a separate math region below the guess definitions. This tells Mathcad that what follows is a system of constraint equations. Be sure you don’t type “Given” in a text region.

3. Now enter the constraints (equalities and inequalities) in any order below the word Given. Make sure you use the bold equal symbol (click  on the Boolean toolbar or press Ctrl]=) for any equality. You can separate the left and right sides of an inequality with any of the symbols <, >, , and .

4. Enter any equation that involves one of the functions Find or Minerr below the constraints.

Solve Blocks

Find(z0, z1,...) - Returns values of z0, z1,... that satisfy the constraints in a solve block. z0, z1,... are real or complex scalars, vectors, arrays, or individual elements of vectors equal in number to the number of unknowns in the system. Returns a scalar for a single unknown; otherwise returns a vector of solutions.

Minerr(z0, z1,...) - Returns values of z0, z1,... that come closest to satisfying the constraints in a solve block. z0, z1,... are real or complex scalars, vectors, arrays, or individual elements of vectors equal in number to the number of unknowns in the system. Returns a scalar for a single unknown; otherwise returns a vector of solutions.

Figure 10-6 shows a solve block with several kinds of constraints and ending with a call to the Find function. There are two unknowns. As a result, the Find function here takes two arguments, x and y, and returns a vector with two elements.

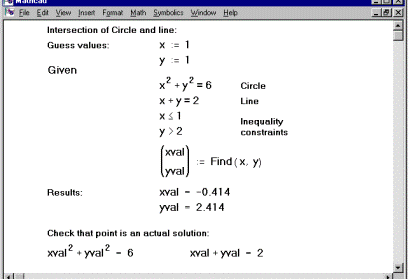
Figure 10-6: A solve block with both equalities and inequalities.

Another example:

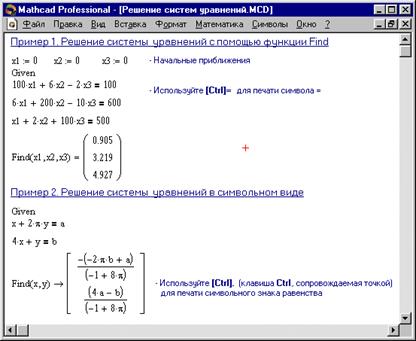
SOLVING LINEAR SIMULTANEOUS EQUATIONS.

There are several ways to solve linear simultaneous equations. One method is to use a given/find solve block. This method is described later, since it can also be used to solve nonlinear equations.

The most common way of solving LINEAR simultaneous equations is to form the equations into matrices, and use matrix algebra. Consider the following four simultaneous equations:

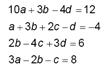
We want to write them in matrix form. We will use matrix B to hold the equation coefficients, and column matrices (vectors) X and Y to hold the variables and equation results respectively.

We find the solution for X by multiplying the equation by the inverse of the B coefficient matrix:

X = B^-1 * Y

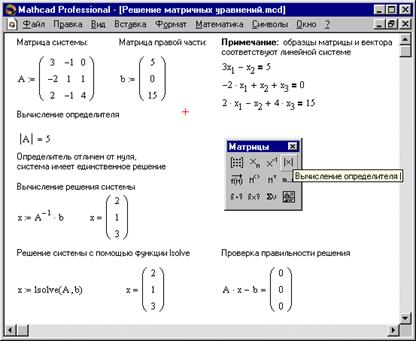
Also Solving a Linear System of Equations can be performed by lsolve function.

lsolve(M, v) - Returns a solution vector x such that 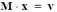. v is a vector having the same number of rows as the matrix M.

An example:

Дата добавления: 2015-10-26