Числа внутренней и внешней устойчивости графа

Рассмотрим теперь число внутренней устойчивости. Если две любые вершины подмножества X’ графа G = (X, U), X’ Í X не смежны, то оно называется внутренне устойчивым. Подмножество y _i Í X графа G = (X, U) называется максимальным внутренне устойчивым подмножеством (МВУП) или независимым (НП), если добавление к нему любой вершины x_i Î X делает его не внутренне устойчивым. Подмножество y _i будет независимым, если

" x_i Î y _i (Г x_i Ç y _i = Æ). (17.8)

Независимые подмножества различаются по числу входящих в них элементов. В произвольном графе G можно выделить семейство всех НП вида y = {y₁, y₂,..., y _s }. Независимые подмножества, содержащие наибольшее число элементов, называются предельными. Тогда число внутренней устойчивости h(G) определяется мощностью предельного НП

h(G) = |max y _i |, y _i Î y. (17.9)

Число внутренней устойчивости h(G) можно связать с хроматическим числом c(G) следующим образом: h(G)c(G) ³ n.

Рассмотрим вопросы построения семейства независимых подмножеств на основе матрицы смежности или ее списка. Данный алгоритм описан А. Кофманом на основе идей предложенных К. Магу. Идея алгоритма построения семейства y = {y₁, y₂,..., y _l } заключается в следующем. В списке смежности графа G определяется строка, имеющая наибольшее число элементов. Если таких строк несколько, то выбирается любая. Для определенной строки i записывается элемент C _i = (x_i + x_k × x_l ×... × x_q), (где знак сложения “ x_i + x_k ” — подразумевает операцию дизъюнкции, а знак умножения “ x_k × x_l ” или “ x_k x_l ” – операцию конъюнкции). Здесь x_i – вершина графа, соответствующая выделенной строке i, а x_k, x_l,..., x_q – вершины, смежные с x_i. Далее в списке смежности исключается строка i, а также элементы с индексом i из всех оставшихся строк списка. Указанная операция соответствует выделению из графа G звездного подграфа с вершиной x_i. В списке снова определяется строка j с наибольшим числом элементов и записывается элемент C _j = (x_j + x_p × x_r ×... × x_v). Далее процесс выполняется аналогично до тех пор, пока в списке для оставшихся строк не будет содержаться ни одного элемента. Затем составляется произведение П = C _i × C _j ×... × C _k, в котором раскрываются скобки, и в полученной сумме выполняется минимизация с учетом выражений

x_i ⁿ = x_i, x_i + x_i +... + x_i = x_i; x_i + 1 = 1; x_i + x_i x_j = x_i. (17.10)

Для выделения семейства y необходимо в выражении, полученном после минимизации, для каждого элемента суммы найти не включенные в него вершины графа, которые образуют максимальные НП.

Методика определения МНП используется для раскраски вершин графа G.

Из рассмотренного алгоритма следует, что раскраску можно интерпретировать как разбиение всех вершин графа на независимые подмножества. Если бы граф имел систему МНП, состоящих из различных вершин, то раскраска соответствовала бы покрытию вершин G системой МНП. Но одни и те же вершины графа могут принадлежать различным МНП. В этой связи существует конечное множество различных допустимых раскрасок, так как вершину, принадлежащую разным МНП, можно окрасить в разные цвета.

Если получено семейство МНП, то можно построить матрицу M = ||m _i,j ||_n×w, где

w – число МНП в семействе y. Тогда задачу раскраски сводят к нахождению наименьшего числа строк, покрывающих все ее столбцы единицами.

Например, для графа G (рис. 17.1) матрицу M можно записать следующим образом:

		x 1	x 2	x 3	x 4	x 5	x 6	x 7
M =	y1								.
y2
y3
y4
y5

Проанализировав данную матрицу, можно отметить, что минимальное число строк, покрывающих все столбцы матрицы, равно трем. Это строки y₁ (покрываются столбцы x ₁, x ₅, x ₆ и x ₇), y₅ (покрываются столбцы x ₃, x ₄), а также либо строка y₃ (покрываются столбцы x ₂, x ₆), либо строка y₄ (покрываются столбцы x ₂, x ₄).

Таким образом, можно выполнить следующую раскраску графа: вершины x ₁, x ₅, x ₆ и x ₇ – первый цвет; вершины x ₃, x ₄ – второй цвет; вершина x ₂ – третий цвет.

Рассмотрим алгоритм определения внешне устойчивого подмножества.

Пусть исследуемый объект задан в виде неориентированного графа G = (X, Г x), который можно рассматривать как пару, образованную множеством Х и многозначным отображением Г х множества Х в себя. Х = { x ₁, x ₂,..., x_n } – множество вершин графа, Г х_i = { x_k, x_e,..., x_p } определяет множество вершин x_k, x_e,..., x_p, смежных с вершиной x_i, другими словами, определяет ребра графа (x_i, x_k), (x_i, x_e),..., (x_i, x_p); .

Подмножество вершин M _i Í Х графа G называется внешне устойчивым, если

(" x Ï M _i) (G x Ç M _i ¹ Æ). (17.11)

Внешне устойчивое подмножество (ВУП) называется минимальным, если удаление из него произвольной вершины делает его внешне неустойчивым. В каждом графе можно выделить семейство М = {M₁, M₂,..., M _i } минимально внешне устойчивых подмножеств (МВУП). Элементы семейства М отличаются друг от друга по виду и количеству входящих в них элементов. Мощность МВУП, содержащего наименьшее число вершин, называется числом внешней устойчивости (b(G)).

Рассмотрим алгоритм получения минимального внешне устойчивого подмножества и наметим путь получения семейства МВУП.

Для задания графов будем использовать структурные числа. Система А, не содержащая одинаковых столбцов a_i и одинаковых элементов a (q, i) в каждом столбце, называется структурным числом.

A = { a ₁, a ₂,..., a_n }, a_i ¹ a_j, a_q = { a (1, q), a (2, q),..., a (m, q)}; a (i, q) ¹ a(j, q).

Столбцам структурного числа (СЧ) можно поставить в соответствие покрывающие деревья графа, а элементам столбцов СЧ – номера соответствующих деревьев. СЧ А имеет геометрическое изображение в виде графа G = (X, Г x), Х = { x ₁, x ₂,..., x_n }, если существует разложение А на простые сомножители P₁, P₂,..., P _{n -1} и произвольный элемент a_i Î P _i встречается не более чем в двух сомножителях. Если каждый P _i записать в виде номеров ребер, смежных вершине x_i, то СЧ графа G примет вид А = P₁, P₂,..., P _{n -1}. Произведение элементов P _i позволит получить СЧ в виде матрицы, где каждый столбец соответствует номерам ребер покрывающего дерева.

Граф G будем задавать в виде преобразованного структурного числа (ПСЧ).

A = Q₁, Q₂,..., Q _n; Q _i = [ i ][ j ₁, j ₂,..., j_l ] = [ i ][Q’ _i ].

Сомножитель Q _i соответствует вершине x_i графа G; i – индекс x_i; Q’ _i = j ₁, j ₂,..., j_l – последовательность индексов вершин, смежных x_i.

Для графа G (рис. 17.7)

Рис 17.7. Граф G

преобразованное структурное число запишется следующим образом:

А =	[1]	[2, 3, 4, 5]	.
[2]	[1, 5, 6]
[3]	[1, 4, 7]
[4]	[1, 3, 6]
[5]	[1, 2, 7]
[6]	[2, 4]
[7]	[3, 5]

Очевидно, что такая запись идентична той, что получилась бы, если бы мы использовали списочное задание графа. Таким образом, преобразованное структурное число А (ПСЧ) это не что иное как список смежности рассматриваемого графа. При этом, для задания графа достаточно n – 1 строк вида Q _i. В связи с вышесказанным в дальнейшем при решении практических задач будем считать равнозначным обозначение A (т.е. преобразованное структурное число) и R_L (т.е. список смежности).

Введем понятие расширенной алгебраической производной ПСЧ, которую запишем следующим образом:

– исключена строка Q _i, а также элементы i и j ₁, j ₂,..., j_l из Q’ _k частей оставшихся строк А.

Указанная операция соответствует удалению из графа G звездного подграфа с вершиной x_i, а также ребер, соединяющих вершины смежные x_i. Вершины, удаленные после взятия производной, будем записывать так: X’ = { i, j ₁, j ₂,..., j_l }. Причем X’ Í X.

На основе введенной операции взятия расширенной алгебраической производной сформулируем алгоритм построения минимального внешне устойчивого подмножества M _i Í M. Основная идея алгоритма заключается в следующем. В ПСЧ определяется строка Q _i, у которой |Q’ _i | максимальна. Если таких строк несколько, то выбирается любая. Далее определяется расширенная алгебраическая производная и записывается подмножество X’ = { x_i, x_k, x_l,..., x_q } (вершины x_k, x_l,..., x_q соответствуют элементам Q’ _i). Затем производится сравнение Х с Х’. Если Х’ = Х, то вершина x_i образует внешне устойчивое подмножество M1. В противном случае в ПСЧ A’ снова определяется строка Q _j, у которой |Q’ _j | максимальна. Если таких строк несколько, то выбирается строка Q _s, которая имеет максимальное число элементов, не вошедших в подмножество Х’ на предыдущем шаге. Находится 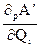и записывается подмножество X’’. Если X’’ = Х, то вершины x_i и x_j образуют внешне устойчивое подмножество M1 = { x_i, x_j }. Если нет, то процесс повторяется аналогично, пока на некотором l шаге X^{( l )} = X. Для построения семейства М необходимо аналогичные операции над ПСЧ выполнять последовательно с каждой строкой с просмотром всех ответвлений.

Запишем алгоритм построения минимального внешне устойчивого подмножества множества вершин G.

1°. Запись по графу G преобразованного структурного числа А.

2°. Выбор в А строки Q _i c |Q’ _i | = max.

3°. Определение и получение Х’.

4°. Сравнение X’ с Х. Если |X’| = |X|, то М₁ = { x_i } и переход к 6°. Иначе к 5°.

5°. Выбор в ПСЧ строки j с максимальным Q’ _j, j: = i и переход к 3°.

6°. Выделено внешне устойчивое подмножество. Конец работы алгоритма.

Работу алгоритма покажем на примере графа G (рис. 17.7). В ранее записанном ПСЧ А выделим строку Q₁, т.к. часть Q’₁ содержит наибольшее число элементов. Определим и получим новое ПСЧ

А’ =	[2]	[6]	.
[3]	[7]
[4]	[6]
[5]	[7]
[6]	[Æ]
[7]	[Æ]

Выделенное подмножество – X’ = { x ₁, x ₂, x ₃, x ₄, x ₅}. Граф, соответствующий A’, показан на рис. 17.8.

Рис. 17.8. Преобразованный г раф G

Мощность X’ не равна мощности Х. Следовательно, вершину x ₁ относим в М₁ и продолжаем процесс получения внешне устойчивого подмножества. На втором шаге определяем строки Q₂, Q₃, Q₄, Q₅. Так как мощность этих строк одинакова, мы можем выбрать любую, например строку Q₂. После этого вычисляем и получаем:

А’’ =	[3]	[7]	.
[4]	[Æ]
[5]	[7]
[6]	[Æ]
[7]	[Æ]

Теперь X’’ = { x ₁, x ₂, x ₃, x ₄, x ₅, x ₆}. Величина |X’’| ¹ |X|, следовательно, вершину x ₂ относим к М₁ и алгоритм продолжает работу. Рассматриваем строки Q₃ и Q₅. Выбираем любую из них, например Q₃, и определяем значение . В результате получим

А’’ =	[4]	[Æ]	.
[5]	[Æ]
[6]	[Æ]
[7]	[Æ]

X’’’ = { x ₁, x ₂, x ₃, x ₄, x ₅, x ₆, x ₇, x ₈} = X. Следовательно, получили внешне устойчивое подмножество M = { x ₁, x ₂, x ₃}.

Теорема 17.2. Подмножество М _i, полученное по алгоритму, является минимальным внешне устойчивым подмножеством.

Доказательство. Покажем, что М _i есть внешне устойчивое подмножество. Предположим, что М _i не является внешне устойчивым, т.е. элементы подмножества вершин М _i совместно не смежны оставшимся вершинам графа. Это говорит о том, что на конечном l шаге работы алгоритма X^{( l )} ¹ X, что противоречит условию алгоритма. Так как алгоритм заканчивает работу, когда X^{( l )} ¹ X, то М _i является внешне устойчивым подмножеством.

Покажем теперь, что М _i Ì М является минимальным внешне устойчивым подмножеством. Предположим, что существует М _j такое, что М _j Ì М _i, т.е. существует, по крайней мере, один элемент x_b Î X, после удаления которого из М _i, подмножество М _j будет внешне устойчивым. Другими словами, алгоритм после получения внешне устойчивого подмножества продолжит работу и выделит М _i É М _j, что противоречит структуре алгоритма. Следовательно, М _i есть минимальное внешне устойчивое подмножество.

Для нахождения числа внешней устойчивости необходимо выделить семейство минимальных внешне устойчивых подмножеств и определить в нем наименьшее по мощности подмножество.

Существуют графы, которые содержат некоторое подмножество X’ Í X вершин, причем это подмножество является одновременно внутренним и внешне устойчивым. Подмножества такого типа называются ядрами графа.

Теорема 17.3 Если граф G = (X, U) имеет ядро, то его числа устойчивости удовлетворяет условию

n(G) ³ b(G). (17.12)

Например, в графе G (рис 3.7) подмножество вершин { x ₃, x ₅, x ₆} является ядром, так как оно одновременно и внешне и внутренне устойчиво. Причем h(G)= 3 = b(G).

Дата добавления: 2015-10-26