Задания для самостоятельной работы. 1. Для графа g = (x, U) построить матрицу и список расстояний.

1. Для графа G = (X, U) построить матрицу и список расстояний.

2. Для произвольного графа G = (X, U) построить его отображение в координатную решетку G _r, матрицу расстояний, матрицу геометрии, а также подсчитать суммарную длину ребер.

3. Для произвольного графа определить диаметр и радиус графа.

4. Для произвольного графа определите центр графа.

5. Определите в произвольном графе G длиннейшие простые цепи и число протяженности.

6. Постройте произвольный граф на 10 вершин, отобразите его в решетку и определите расстояние между его вершинами.

7. Постройте словесный алгоритм определения матрицы геометрии.

8. Запишите псевдокод алгоритма определения матрицы геометрии.

9. Приведите структурную схему алгоритма определения матрицы геометрии по рисунку графа.

10. Приведите словесный алгоритм отображения графа в координатную решетку.

Понятия расстояния в графе, а также связанные с ним понятия метрики графа, длины цепи, матриц расстояний и геометрии являются базовыми понятиями при решении широкого круга оптимизационных задач, связанных с топологией графа.

Деревья

Связный граф без циклов называется деревом и обозначается T = (X, U), |X| = n. Любое дерево T имеет n – 1 ребро. Начальная вершина называется корнем, из которого выходят ребра – ветви дерева. Очевидно, что в дереве любые две вершины x_i, x_j связаны единственной цепью. В любом связном графе G можно выделить произвольное дерево Т. В любом дереве порядка n ³ 2 имеется не менее двух концевых вершин.

Теорема 16.8. Пусть Т – граф из n вершин. Следующие утверждения эквивалентны:

· Т является деревом,

· Т не содержит циклов и имеет n – 1 ребер,

· Т связен и имеет n – 1 ребер,

· Т связен и каждое его ребро является мостом,

· любые две вершины графа Т соединены ровно одной простой цепью,

· Т не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один цикл.

Для задач конструкторского и технологического проектирования наибольший интерес представляют деревья, у которых число вершин равно числу вершин графа, из которого выделено это дерево. Такие деревья называются покрывающими (ПД) или остовными. На рис 16.33 показан полный граф K₄ и все его 16 ПД.

1-й ряд

2-й ряд

3-й ряд

4-й ряд

Рис. 16.33. Граф K₄ и его покрывающие деревья

Отметим, что здесь всего 4 различных покрывающих дерева. Остальные графы в каждом ряду одинаковые, только нарисованы по-разному.

В связном графе G удаление одного ребра, принадлежащего некоторому выбранному циклу, не нарушает связности оставшегося графа. Можно применять эту процедуру до тех пор, пока в G не останется ни одного цикла. В результате получим дерево, связывающее все вершины G. Оно является остовным (покрывающим) деревом или остовом или каркасом графа.

Граф, в котором число ребер не меньше чем число вершин, содержит цикл. Число ребер m произвольного графа G = (X, U), |X| = n, |U| = m, которые необходимо удалить для получения каркаса, не зависит от последовательности их удаления.

Например, на рис. 16.34, а показан граф G, а на рис. 16.34, б его каркас (остовное дерево).

а б

Рис. 16.34. Граф G (а) и его остовное дерево (б)

Утверждение 16.4. Всякий ациклический подграф G’ = (X’, U’) произвольного графа G = (X, U), X’ Í X, U’ Í U содержится в некотором каркасе O графа G (O = (X, U’), G = (X, U), U’ Í U).

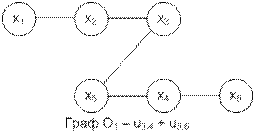
Утверждение 16.5. Если O₁ = (X₁, U₁) и O₂ = (X₂, U₂) два каркаса графа G = =(X, U) (X = X₁ = X₂, U₁ Í U, U₂ Í U), то для любого ребра u_i Î U₁ графа O₁ существует такое ребро u_j Î U₂ графа O₂, что граф O₁ - u_i + u_j также является каркасом. Например, имеем граф G (рис. 16.35, а) и два каркаса этого графа O₁ (рис. 16.35, б) и O₂ (рис. 16.35, в). Пусть ребро u_i = u _3,4, а ребро u_j = u _5,6, ребро u_i Î U₁ графа O₁ и ребро u_j Î U₂ графа O₂. Тогда граф O₁ - u_i + u_j = O₁ - u _3,4 + u _5,6 также будет каркасом (рис. 16.35, г).

а б

в г

Рис. 16.35. Граф G и его каркасы

Теорема 16.9 (Кэли). Существует ровно n^n-2 различных помеченных деревьев с n вершинами.

Следствие 16.1. Число остовных деревьев в K_n равно n^n-2.

Множество деревьев графа называется лесом. На рис. 16.36 показан лес, состоящий из 3 деревьев T1 - T3.

Рис. 16.36. Множество деревьев графа

Задачи выделения эйлеровых и гамильтоновых циклов и покрывающих деревьев связаны с задачами о лабиринте, коммивояжере и с построением цепей, циклов, маршрутов минимальной стоимости.

Задача о лабиринте в терминах теории графов формулируется как задача отыскания в связном графе G = (X, U) такого маршрута, который начинается в заданной вершине x_i Î X и приводит в искомую вершину x_j Î X, причем маршрут должен содержать кратчайшее число ребер.

Пусть нам необходимо проложить сеть проводов, связывающих n терминалов вычислительной аппаратуры, причем так, чтобы из одного терминала можно было связаться с любым другим. Если из экономических соображений требуется, чтобы количество затраченного провода было минимально, то граф, вершины которого соответствуют терминалам, а ребра соединяющим их проводам, должен быть деревом. Задача состоит в определении одного из n^n-2 возможных деревьев, соединяющих терминалы, с минимизацией числа проводов. На языке теории графов эту задачу можно сформулировать следующим образом. Пусть G = (X, U) связный граф и каждому ребру u_i Î U ставится в соответствие некоторое неотрицательное n(u_i), называемое его мерой или весом. Необходимо найти алгоритм построения покрывающего дерева Т, у которого сумма мер, взятая по всем ребрам, минимальна. Такие деревья будем называть кратчайшими покрывающими деревьями (КПД). Графы с весами на ребрах или вершинах будем называть взвешенными.

Запишем алгоритм Краскала для построения кратчайшего покрывающего дерева.

1. Пусть задан граф G = (X, U), для которого нужно построить кратчайшее покрывающее дерево. Строим граф G₁ = O_п + u ₁, присоединяя к пустому графу O_п на множестве вершин X ребро u ₁ Î U минимального веса.

2. Если граф G _i уже построен и i < n – 1, то строим граф G _{i +1} = G _i + u_{i +1},

где u_{i +1} – ребро графа G, имеющее минимальный вес среди ребер, не входящих в G _i и не составляющих циклов с ребрами из G _i. При i = n – 1, переход к пункту 3.

3. Конец работы алгоритма.

Теорема 16.10. При i < n – 1 граф G _{i +1} можно построить. Граф G _{n -1} является каркасом с минимальным весом ребер в графе G.

Например, пусть задан граф с G весами на ребрах (рис. 16.37).

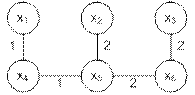
а б

Рис. 16.37. Взвешенный граф G(а); каркас графа G (б)

Согласно алгоритму Краскала выбираем сначала ребро u _1,4 с весом 1. Далее берем ребро u _1,5 с весом 1. Затем среди оставшихся ребер с минимальным весом есть ребро u _4,5, однако оно не пригодно для каркаса, т.к. образует цикл с ребрами u _1,4 и u _1,5. Далее выбираем ребра u _3,6 и u _5,6 с весом 2. Итак, каркас с минимальным весом равным 8 построен (рис. 16.37, б)

Приведем логическую схему алгоритма (ЛСА) Краскала решения данной задачи:

A₀A₁¯²¯¹A₂p₁­¹p₂­²A_к,

здесь А₀ – оператор начала;

А₁ – оператор, устанавливающий i = 1;

А₂ – оператор, выбирающий ребро u_i с наименьшим весом;

р₁ – проверка логического условия несовпадения ребра u_i с предыдущим и необразования цикла с предыдущими ребрами. При p₁ = 0, i = i + 1 переход к A₂, при p₁ = 1 переход к p₂;

p₂ – проверка логического условия, что мощность выбранных ребер равна n – 1. При p₂ = 0, i = i + 1 переход к А₂, при p₂ = 1 переход к А_к;

А_к – оператор конца алгоритма.

Опишем алгоритм Прима построения кратчайшего покрывающего дерева (КПД) на взвешенном по ребрам графе. Алгоритм основан на разрастании поддеревьев. Дерево T’ = (X’, U’) является поддеревом T = (X, U), если X’ Í X, U’ Í U. Причем поддерево T’ может состоять и из одной вершины. Поддерево Т’ последовательно разрастается за счет прибавления ребер (x_i, x_j), (x_i Î T, x_j Ï T’). Каждое добавляемое ребро должно иметь наименьший вес. Процесс продолжается, пока число ребер в T’ не станет равным n – 1. Покажем работу алгоритма на построении кратчайшего покрывающего дерева в графе G. Пусть граф задан матрицей смежности:

R =								.

Выбираем вершину x ₁ и считаем ее на первом шаге поддеревом T’ = (X’, U’), X’ = { x ₁}, U’ = Æ. Строим упорядоченный список ребер, инцидентных вершине x ₁. Упорядочивание производится по возрастанию веса ребер.

	ui	n(ui)
L=	(1, 2)		.
(1, 3)
(1, 5)

Из списка выбирается ребро (1, 2) (т.е. (x ₁, x ₂)). Производится разрастание поддерева T’ = (X’, U’), X’ = { x ₁, x ₂}, U’ = {(1, 2)}. В список L вносятся ребра, инцидентные вершине x ₂. После этого ребра снова упорядочиваются, и список примет вид

	ui	n(ui)
	(2, 4)		.
L=	(1, 3)
	(2, 5)
	(1, 5)

Выбирается ребро (2, 4) с наименьшим весом и добавляется к поддереву T’, если оно не образует цикла с ребрами T’. Остальные ребра, объединяющие вершины X’ между собой, удаляются из L; X’ = { x ₁, x ₂, x ₄}, U’ = {(1, 2), (2, 4)}. Проверяется |X’| = |X|, если нет, то выбирается вершина x ₄ и ребра, инцидентные ей, пополняют список L:

	ui	n(ui)
	(4, 3)		.
	(1, 3)
L=	(2, 5)
	(4, 5)
	(4, 6)
	(1, 5)

Продолжая, получаем U’ = {(1, 2), (2, 4), (4, 3), (2, 5), (5, 6)}, |X| = |X’|, процесс окончен, S₁^n-1n(u_i) = 32. На рис. 16.38 кратчайшее покрывающее дерево показано жирными линиями.

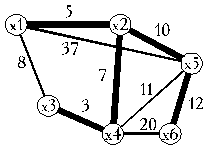
Рис. 16.38. Исходный граф G и его кратчайшее покрывающее дерево

Алгоритмы построения покрывающих деревьев с минимальной суммарной длиной ребер на взвешенных графах основаны на двух принципах:

· каждая изолированная вершина соединяется с ближайшей соседней;

· каждое изолированное поддерево соединяется с ближайшей соседней вершиной (или поддеревом) кратчайшим ребром (или цепью).

Задача построения КПД усложняется, если при соединении множества вершин (контактов цепи) разрешается использование дополнительных точек соединения. В общем виде данная задача формируется так: для заданных x ₁, x ₂,..., x_n точек плоскости построить КПД с n’ ³ n вершинами — и называется задачей Штейнера (ЗШ). Обычно решение ЗШ рассматривают в областях прямоугольной конфигурации. Для n £ 5 известно решение ЗШ, в общем же случае известны условия, которым должны удовлетворять деревья Штейнера (ДШ) и эвристические алгоритмы. Дополнительные точки, вводимые при построении КПД, называют точками Штейнера (ТШ).

Приведем ряд лемм, полученных Фридманом и Меноном, дающих необходимые условия существования и построения ДШ.

Лемма 16.1. Для n вершин, которые должны быть соединены между собой, всегда можно построить ДШ, в котором каждая ТШ g_i соединена по крайней мере с тремя другими.

Лемма 16.2. Для множества вершин { x ₁, x ₂, x ₃}, которые должны быть соединены, координаты ТШ g, минимизирующей S³ _{i = 1} d (g, n_i), будут Sср, Тср и справедливо выражение S³ _{i = 1} d (g, n_i) = 1/2 P(x ₁, x ₂, x ₃), где Sср, Тср – средние значения S _i (i = 1, 2, 3) и T _j (j = 1, 2, 3); P(x ₁, x ₂, x ₃) – длина периметра прямоугольника, построенного на вершинах x ₁, x ₂, x ₃; d (g, n_i) – прямоугольное расстояние между g и n_i.

На рис. 16.39 показан пример, иллюстрирующий условия леммы 16.2 при построении ДШ, соединяющего вершины x ₁, x ₂, x ₃. Точка Штейнера g имеет координаты S g = 3,T g = 5.

Рис. 16.39. Построения дерева Штейнера

Лемма 16.3. Дано ДШ, состоящее из x_i точек плоскости. Пусть ТШ g соединена только с тремя вершинами x ₁, x ₂, x ₃. Тогда g находится внутри прямоугольника, построенного на вершинах x ₁, x ₂, x ₃, и ТШ единственная.

Следствие 16.2. Для заданного множества вершин x ₁, x ₂, x ₃ ДШ содержит одну ТШ g c координатами (Sср, Тср), если она не совпадает ни с одной из вершин x ₁, x ₂, x ₃ и суммарная длина ребер ДШ равна 1/2P(x ₁, x ₂, x ₃).

Лемма 16.4. Дано ДШ на множестве X = { x ₁, x ₂,..., x_n }, а ТШ этого дерева образуют множество G = { g ₁, g ₂,..., g_k }. Если g ₁ Ì G и g_i Î I, то g ₁ содержит элемент g _1.k, соединенный не менее чем с двумя вершинами из I, в противном случае g ₁ пусто. Здесь I — множество точек пересечения линий координатной сетки.

На основе приведенных лемм сформулирована известная теорема.

Теорема 16.11. Дано ДШ на множестве вершин X = { x ₁, x ₂,..., x_n } с множеством ТШ G = { g ₁, g ₂,..., g_k }. Тогда для этого множества существует такое другое ДШ с множеством ТШ G’, что (" g’_i Î G’)(g’_i Î I).

Из рассмотрения теоремы следует метод определения ДШ на основе полного перебора в качестве ТШ всех возможных подмножеств точек I. Очевидно, что такой метод применим только при построении ДШ для небольшого числа ТШ. В этой связи разрабатываются эвристические процедуры построения квазиоптимальных ДШ.

Процедура 1.

1°. Все вершины x_i Î X проектируются на ось S(T).

2°. Расстояние от наименьшей до наибольшей координаты делится пополам, и из этой точки i Î I проводится перпендикуляр (столб Штейнера).

3°. Из каждой вершины x_i Î X опускается перпендикуляр до пересечения со столбом Штейнера.

4°. Построено ДШ. Конец работы алгоритма.

На основе данной процедуры можно предложить следующий алгоритм построения дерева Штейнера.

Итак, во-первых, мы отображаем заданный граф G в координатную решётку, а затем находим координаты всех вершин полученного графа G _r и вычисляем по какой из осей координат разность максимального и минимального значений координат будет максимальной.

После этого проводим перпендикуляр к той оси, относительно которой разность координат меньше. При этом перпендикуляр проводим либо на равном удалении от крайних точек, либо, если количество вершин с одной стороны перпендикуляра значительно превышает число вершин с другой, немного сдвигаем перпендикуляр по оси координат в сторону большего числа вершин.

Полученный таким образом перпендикуляр представляет собой ось или ствол будущего дерева, который затем соединяют отрезками с остальными вершинами графа.

Данный алгоритм очень прост, ВСА равна O(n), но суммарная длина проводников дерева Штейнера далеко не оптимальна.

Процедура 2 (Алгоритм Ханана).

1°. Все множество вершин x_i Î X разбивается на классы S₀, S₁,..., S _i в порядке возрастания координаты S _i так, чтобы у всех вершин одного класса была одинаковая координата S _i.

2°. Анализируется множество вершин класса S₀, и соединяются перпендикуляром все вершины этого множества с точкой S_min оси S.

3°. Образуется множество I’, состоящее из всех точек I, которые были до этого соединены с произвольной вершиной x_i, включая и вершины x_i строящегося ДШ.

4°. Выбирается следующее множество S _{i +1}, имеющее наименьшую координату S. Определяются точка i_m Î I’ и вершина x_j Î S _{i +1}, для которых

d (i_m, x_j) ³ d (i_q, x_j’), " i_q Î I’, " x_j’ Î S _{i +1}.

Другими словами, x_i находится на кратчайшем расстоянии от рассматриваемого фрагмента ДШ в классе S _{i +1}. Точка i_m с координатами (s_m, t_m) соединяется с вершиной x_j с координатами (s_i, t_i) двухзвенной линией. Причем звенья параллельны координатным осям S и T.

5°. Для каждой вершины x_k Î S _{i +1} производятся операции, аналогичные 4°. При этом вершина x_k соединяется с ближайшей в I’.

6°. Пункты 4° и 5° повторяются для всех по порядку множеств S _j до построения ДШ.

Отметим, что существует большое число модификаций описанных процедур. Можно проводить упорядочивание координат не по увеличению S(T), а по уменьшению S(T). Временная сложность алгоритма процедуры 2 составляет O(n²). На рис. 2.39, б показана реализация процедуры 2 с упорядочиванием вершин в 1° в порядке убывания координат S. Суммарная длина ДШ составляет 22 условные единицы, при этом число ТШ равно 2.

Для построения ДШ можно использовать методы поиска или ветвей и границ в зависимости от требований на ВСА.

Заметим, что на основе модели дерева можно описывать любое алгебраическое выражение, например, дерево (рис. 16.40) может моделировать следующие записи:

(2+у)*7, *+2у7, *(2+у)7, 2у+7*, (2+у)7* и т.п.

Запись, где символы операций предшествуют операндам, называется Польским выражением или Польской записью. Это – *+2у7. Использование таких моделей позволяет разрабатывать эффективные программы и алгоритмы преобразования алгебраических выражений.

Рис. 16.40. Пример записи алгоритма на основе модели дерева

Дата добавления: 2015-10-26