
Читайте также:
|
Пример 1. Пусть задан граф G = (X, U). Найти с помощью алгоритма Форда кратчайшие пути в заданном графе G от фиксированной вершины до всех остальных.
Решение: Рассмотрим матрицу смежности графа G:
| M | M | M | M | . | ||||||
| M | M | M | M | |||||||
| M | M | M | M | |||||||
| R=4 | M | M | M | M | ||||||
| M | M | M | M | M | ||||||
| M | M | |||||||||
| M | M | M | ||||||||
| M | M | M | M | |||||||
| M | M |
1.1. В качестве фиксированной вершины выбираем вершину x 1. Тогда ее вес V(1) = 0, а веса всех остальных вершин: V(2) = V(3) = … = V(9) = ¥ = M.
1.2. Просматриваем первую строку матрицы смежности и выбираем поочередно все вершины, не помеченные литерой M. В результате мы сформировали следующий список вершин: x 2, x 7, x 8, x 9.
1.3. Для каждой из вершин, входящих в полученный список, проверяем истинность неравенства (1.8):
V(2) = ¥ > 0 + 10 = 10; V(7) = ¥ > 0 + 3 = 3; V(8) = ¥ > 0 + 6 = 6;
V(9) = ¥ > 0 + 12 = 12.
Значения весов для вершин x 3, x 4, x 5, x 6 не изменяются.
Теперь произведем пересчет индексов для вершин смежных с x 1, с учетом пути через другие смежные вершины.
1.4. Производим пересчет весов для сформированного списка вершин:
для вершины x 2:
- V(2) > V(7) + r27 ® 10 > 3 + 2 ─ неравенство истинно, следовательно, вес вершины изменяется: V(2)1 = 5,
- V(2) > V(9) + r29 ® 10 > 1 + 13 ─ неравенство ложно, следовательно, вес вершины не изменяется;
для вершины x 7:
- V(7) > V(2) + r27 ® 3 > 10 + 2 ─ неравенство ложно, следовательно, вес вершины не изменяется;
- V(7) > V(9) + r79 ® 3 > 12 + 24 ─ неравенство ложно, следовательно, вес вершины не изменяется.
для вершины x 8:
- V(8) > V(9) + r89 ® 6 > 12 + 5 ─ неравенство ложно, следовательно, вес вершины не изменяется;
для вершины x 9:
- V(9) > V(2) + r29 ® 12 > 10 + 13 ─ неравенство ложно, следовательно, вес вершины не изменяется,
- V(9) > V(7) + r79 ® 12 > 3 + 24 ─ неравенство ложно, следовательно, вес вершины не изменяется,
- V(9) > V(8) + r89 ® 12 > 6 + 5 ─ неравенство истинно, следовательно, вес вершины изменяется: V(9)1 = 11.
1.5. Проверка условия: все ли вершины помечены.
Произведем пересчет индексов для вершин, несмежных с фиксированной вершиной x 1.
2.1. Вычислим значение веса вершины x 3, его можно найти через x 2, x 4, x 6 или x 9. Однако значения весов вершин x 4 и x 6 нам пока не известны, поэтому производим расчет через вершины x 2 и x 9:
- V(3) > V(2) + r23 ® ¥ > 5 + 18 - неравенство истинно, следовательно, вес вершины изменяется: V(3)1 = 23,
- V(3) > V(9) + r39 ® 23 > 11 + 7 ─ неравенство истинно, следовательно, вес вершины изменяется: V(3)2 = 18.
2.2. Вычислим значение веса вершины x 4, его можно найти через x 3, x 5, x 6 или x 7. Однако значения весов вершин x 5 и x 6 нам пока не известны, поэтому производим расчет через вершины x 3 и x 7:
- V(4) > V(3) + r34 ® ¥ > 18 + 25 ─ неравенство истинно, следовательно, вес вершины изменяется: V(4)1 = 43,
- V(4) > V(7) + r47 ® 43 > 3 + 4 ─ неравенство истинно, следовательно, вес вершины изменяется: V(4)2 = 7.
2.3. Вычислим значение веса вершины x 5, его можно найти через x 4, x 6 или x 8. Однако значение веса вершины x 6 нам пока не известно, поэтому производим расчет через вершины x 4 и x 8:
- V(5) > V(4) + r45 ® ¥ > 7 + 5 ─ неравенство истинно, следовательно, вес вершины изменяется: V(5)1 = 12,
- V(5) > V(8) + r58 ® 12 > 6 + 23 ─ неравенство ложно, следовательно, вес вершины не изменяется.
2.4. Вычислим значение веса вершины x 6, его можно найти через x 3, x 4, x 5, x 7, x 8 или x 9:
- V(6) > V(3) + r36 ® ¥ > 18 + 20 ─ неравенство истинно, следовательно, вес вершины изменяется: V(6)1 = 38,
- V(6) > V(4) + r46 ® 38 > 7 + 16 ─ неравенство истинно, следовательно, вес вершины изменяется: V(6)2 = 23,
- V(6) > V(5) + r56 ® 23 > 12 + 10 ─ неравенство истинно, следовательно, вес вершины изменяется: V(6)3 = 22,
- V(6) > V(7) + r67 ® 22 > 3 + 17 ─ неравенство истинно, следовательно, вес вершины изменяется: V(6)4 = 20,
- V(6) > V(8) + r68 ® 20 > 6 + 15 ─ неравенство ложно, следовательно, вес вершины не изменяется.
- V(6) > V(9) + r69 ® 20 > 11 + 9 ─ неравенство ложно, следовательно, вес вершины не изменяется,
3. Конец работы алгоритма.
Алгоритм Форда дает кратчайшее расстояние от вершин до фиксированной вершины, а сами цепи не определяет.
Для определения цепи от выбранной вершины до фиксированной воспользуемся равенством V(j) ─ V(i) = ri,j.
Например, найдем путь от x 6 до x 1. Ищется предпоследний шаг при пересчете индекса V(6). Это x 6 ─ x 7. Затем для x 7 определяется вершина пересчета. Это x 6 - x 1. Следовательно, кратчайший путь x 6 – x 7 ─ x 1, а – кратчайшее расстояние между вершинами x 1 и x 6 определено ранее V(6) = 20.
Пример 2. Пусть задан граф G = (X, U). Найти с помощью алгоритма Дейкстра кратчайшие пути в заданном графе G от фиксированной вершины до всех остальных.
Решение: Рассмотрим матрицу смежности графа G:
| . | ||||||||||
| R=4 | ||||||||||
Постоянные пометки будем обозначать *, остальные временные.
1°. l (x 1) = 0*. l (xi) = ¥, " xi ¹ x 1, p = x 1.
В качестве начальной вершины принимаем вершину x 1. Всем остальным вершинам графа присваиваем метки l (xi) = ¥.
Первая итерация
2°. Г(p) = Г(x 1) = { x 2, x 7, x 8, x 9}. Возьмем вершину x 2 и из выражения (15.9) получим:
l (x 2) min[ l (x 2), l (x 1) + r(x 1, x 2)] = min[¥, 0* + 10] = 10.
Аналогично вычисляем значения меток для других вершин, смежных с вершиной x 1: l (x 7) = 3, l (x 8) = 6, l (x 9) = 12.
3°. В списке вершин графа выберем вершину, имеющую минимальное значение метки: Min[ x 2, x 7, x 8, x 9, x 3, x 4, x 5, x 6] = min[10, 3, 6, 12, ¥, ¥, ¥, ¥] = 3 ─ соответствует вершине x 7.
4°. Вершина x 7 получает постоянную пометку l(x 7) = 3*, p = x 7.
5°. Не все вершины имеют постоянные пометки, переходим к п. 2°.
Вторая итерация
2°. Г(p) = Г(x 7) = { x 2, x 4, x 6, x 9} ─ все пометки временные. Из выражения (1.9) вычисляем:
l (x 2) = min[ l (x 2), l (x 7) + r(x 7, x 2)] = min[10, 3* + 2] = 5.
Аналогично l (x 4) = 7, l (x 6) = 17, l (x 9) = 12.
3°. Min[ x 2, x 4, x 6, x 8, x 9, x 3, x 5] = min[5, 7, 17, 6, 12, ¥, ¥] = 5 ─ соответствует вершине x 2.
4°. Вершина x 2 получает постоянную пометку l (x 2) = 5*, p = x 2.
5°. Перейдем к п. 2°, т.к. не все вершины имеют постоянные пометки.
Третья итерация
2°. Г(p) = Г(x 2) = { x 1, x 3, x 7, x 9}, только x 3 и x 9 имеют временные пометки. Из выражения (15.9) получим l (x 3) = min[¥, 5* + 18] = 23, l (x 9) = min[12, 5* + 13] = 12.
3°. Min[ x 3, x 4, x 8, x 6, x 9, x 5] = min[23, 7, 6, 17, 12, ¥] = 6 ─ соответствует вершине x 8.
4°. Вершина x 8 получает постоянную пометку l (x 8) = 6*, p = x 8.
5°. Перейдем к п. 2°, так как. не все вершины имеют постоянные пометки.
Четвертая итерация
2°. Г(p) = Г(x 8) = { x 9, x 6, x 5}, x 5 и x 9 имеют временные пометки. Из выражения (15.9) получим:
l (x 5) = min[¥, 6* + 23] = 29, l (x 9) = min[12, 6* + r(x 8, x 9)] = 11.
3°. Min[ x 5, x 9, x 3, x 4, x 5] = min[29, 11, 23, 7, 29] = 7 ─ соответствует вершине x 4.
4°. Вершина x 4 получает постоянную пометку l (x 4) = 7*, p = x 4.
5°. Переход к п. 2°.
Пятая итерация
2°. Г(p) = Г(x 4) = { x 3, x 6, x 5}. l (x 3) = 23, l (x 6) = 17, l (x 5) = 12.
3°. Min[ x 5, x 6, x 9, x 3] = min[12, 17, 11, 23] = 11.
4°. Вершина x 9 получает постоянную пометку l (x 9) = 11*, p = x 9.
5°. Переход к п. 2°.
Шестая итерация
2°. Г(p) = Г(x 9) = { x 3, x 6} (берем только непомеченные вершины).
(x6) = min[ l (x 6), l (x 9) + r(x 6, x 9)] = [17, 11* + 9] = 17, l (x 3) = 18.
3°. Min[ x 5, x 6, x 3] = min[12, 17, 18] = 12.
4°. Вершина x 5 получает постоянную пометку l (x 5) = 12*, p = x 5.
5°. Переход к п. 2°.
Седьмая итерация
2°. Г(p) = Г(x 5) = { x 6}.
l (x 6) = min[ l (x 6), l (x 5) + r(x 5, x 6)] = [17, 12* + 10] = 17.
3°. Min[ x 6, x 3] = min[17, 18] = 17.
4°. Вершина x 6 получает постоянную пометку l (x 6) = 17*, p = x 6.
5°. Переход к п. 2°.
Восьмая итерация.
2°. Г(p) = Г(x 3) = Æ.
l (x 3) = min[18] = 18, p = x 3. Все вершины помечены.
Итак, получили кратчайшие пути от вершины x 1 до всех остальных:
x 1 ® x 2(5*), x 1 ® x 3(18*), x 1 ® x 4(7*), x 1 ® x 5(12*), x 1 ® x 6(17*), x 1 ® x 7(3*), x 1 ® x 8(6*), x 1 ® x 9(11*);
x 1 ® x 7 ® x 2 ® x 3(18*), x 1 ® x 7 ® x 2(5*), x 1 ® x 8(6*), x 1 ® x 8 ® x 9(11*), x 1 ® x 7 ® x 6(17*), x 1 ® x 7 ® x 4 ® x 5(12*), x 1 ® x 7 ® x 4(7*).
Длину цепи, т.е. суммарную стоимость весов пройденных ребер, можно получить при помощи описанной ранее рекурсивной процедуры.
Например: x 1 ® x 3(18*), сумму 18 дает вершина x 9 с ребром { x 9 ─ x 3}:
имеем x 3 ® x 9(11*), сумму 11 дает вершина x 8 с ребром { x 8 ─ x 9}.
имеем x 3 ® x 9 ® x 8(6*), сумму 6 дает вершина x 1 с ребром { x 1 ─ x 8}.
Тогда имеем кратчайший путь x 3 ® x 9 ® x 8 ® x 1 длиной 18.
Результат построения кратчайших путей в графе G показан на рис. 15.33.
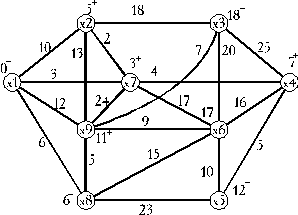
Рис. 15.33. Граф G
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Какой граф называется взвешенным?
2. Как определяется кратчайшая цепь в графе?
3. Что представляет собой алгоритм Форда?
4. Для чего используется алгоритм Форда?
5. Какова сложность алгоритма Форда?
6. На чем основан метод Дейкстры?
7. Для чего используется алгоритм Дейкстры?
8. Какова сложность алгоритма Дейкстры?
9. Как определяется последовательность прохождения вершин в кратчайшей цепи?
10. В каком случае алгоритмы Форда и Дейкстры не позволяют найти кратчайший по стоимости путь?
Дата добавления: 2015-10-26; просмотров: 159 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Алгоритм Форда | | | Эйлеровы и гамильтоновы цепи и циклы |