
Читайте также:
|
Пример 1. Для графа, показанного на рис. 15.15, записать множества ориентированных и неориентированных ребер и дуг.

Рис. 15нка 1.15, граф содержит 8 вершин и 15 ребер: |X| = 8; |U| =15,тогда множество реберU =  È
È 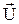 Ç
Ç 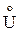 включает в себя следующие подмножества:
включает в себя следующие подмножества:  = { u 1, u 4, u 6, u 10, u 12, u 14};
= { u 1, u 4, u 6, u 10, u 12, u 14}; 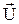 = { u 2, u 3, u 5, u 7, u 9, u 13};
= { u 2, u 3, u 5, u 7, u 9, u 13}; 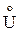 = { u 8, u 11, u 15}.
= { u 8, u 11, u 15}.
Пример 2. Привести пример мультиграфа с мультичислом, равным 4.
Ответ: Мультиграф, удовлетворяющий заданным требованиям, приведен на рис. 15.16.

Рис. 15.16. Искомый мультиграф
Пример 3. Пусть граф G = (X, U) (рис. 15.17)задан графическим способом. Задать тот же граф аналитическим и матричным способом.

Рис. 15.17. Граф G
Решение: Граф, заданный на рис. 15.17, можно задать аналитическим способом следующим образом:  |X| = 7; X = { x 1, x 2, x 3, x 4, x 5, x 6, x 7}; Г = {Г x 1, Г x 2, Г x 3, Г x 4, Г x 5, Г x 6, Г x 7}; Г x 1 = { x 2, x 3, x 4, x 5, x 7}; Г x 2 = { x 1, x 3, x 4, x 5, x 6, x 7}; Г x 3 = { x 1, x 2, x 5, x 6, x 7}; Г x 4 = { x 1, x 2}; Г x 5 = { x 1, x 2, x 3, x 6}; Г x 6 = { x 2, x 3, x 5}; Г x 7 = { x 1, x 2, x 3}.
|X| = 7; X = { x 1, x 2, x 3, x 4, x 5, x 6, x 7}; Г = {Г x 1, Г x 2, Г x 3, Г x 4, Г x 5, Г x 6, Г x 7}; Г x 1 = { x 2, x 3, x 4, x 5, x 7}; Г x 2 = { x 1, x 3, x 4, x 5, x 6, x 7}; Г x 3 = { x 1, x 2, x 5, x 6, x 7}; Г x 4 = { x 1, x 2}; Г x 5 = { x 1, x 2, x 3, x 6}; Г x 6 = { x 2, x 3, x 5}; Г x 7 = { x 1, x 2, x 3}.
Очевидно, что такой способ задания содержит слишком много избыточной информации. Для устранения этого недостатка достаточно использовать Г xn -1 ─ образ и не включать в Г xi -1элементы хi,определяющие Г xi.
Тогда получим: Г x 1 = { x 2, x 3, x 4, x 5, x 7}; Г x 2 = { x 3, x 4, x 5, x 6, x 7}; Г x 3 = { x 5, x 6, x 7}; Г x 4 = Æ; Г x 5 = { x 6}; Г x 6 = Æ; Г x 7 = Æ.
Граф, изображенный на рис. 15.17, можно задать также в виде специальной матрицы (матрицы смежности).
 .
.
При этом для задания неориентированного графа вполне достаточно треугольной матрицы типа R’:
 .
.
Для любого графа, в том числе заданного на рис. 15.17, можно задать еще одну специальную матрицу ─ матрицу инцидентности. Любой элемент ipq матрицы инцидентности будет равен 1, в случае если p -я вершина в исходном графе инцидентна q -му ребру. Таким образом, матрица инцидентности для графа, заданного на рис. 15.17, примет следующий вид:
 .
.
Пример 4. Привести примеры подграфа, суграфа и дополнения до полного для графа, заданного на рис. 15.17.
На рис.15.18. изображен подграф G’ графа G, полученный удалением из графа G вершин x 2, x 3 и инцидентных им ребер.
На рис.15.19. изображен граф G’ = (X’, U’), являющийся суграфом графа G: |X’| = 7, |U’| = 8.
На рис.15.20. изображен граф  = K \ G являющийся дополнением до полного графа G.
= K \ G являющийся дополнением до полного графа G.

Рис. 15.18. Подграф графа G

Рис.15.19. Суграф графа G

Рис.15.20. Дополнение графа G
Пример 5. Для графа G, заданного на рис. 15.21 а), построить двойственный ему граф GS.

Рис. 15.21. а) Пример графа G
Решение: Зададим смежностный (двойственный) граф GS = (U, V) для графа G = (X, U). Для построения GS по G на каждом ребре ui Î U графа G выбирают среднюю точку и считают ее вершиной ui Î U графа GS. Граф G содержит 8 ребер, следовательно, двойственный ему граф Gs будет иметь 8 вершин.
Затем пару (ui, uj) соединяем ребром vk = (ui, uj), если ребра ui, uj имеют общую вершину в G. То есть для графа GS вершина u 1, например, будет иметь общие ребра с вершинами u 2, u 3, u 4, u 7, u 8, так как эти ребра в исходном графе G имели общие вершины (x 1 и x 3). Далее продолжаем строить ребра для других вершин графа Gs.
Ответ: В результате получим следующий двойственный граф GS (рис 15.21 б).

Рис. 15.21. б) Двойственный граф GS
Пример 6. Задать нечеткий граф  = (X,
= (X,  ), у которого X = { х 1, х 2, х 3, х 4, х 5}, a
), у которого X = { х 1, х 2, х 3, х 4, х 5}, a  = {<0,3/(х 1, х 1)>, <0,7/(х 1, х 2)>, <1/(х 1, х 5)>, <0,6/(х 2, х 4)>, <0,4/(х 2, х 5)>, <0,9/(х 3, х 4)>, <0,8/(х 3, х 3)>}.
= {<0,3/(х 1, х 1)>, <0,7/(х 1, х 2)>, <1/(х 1, х 5)>, <0,6/(х 2, х 4)>, <0,4/(х 2, х 5)>, <0,9/(х 3, х 4)>, <0,8/(х 3, х 3)>}.
Решение: Граф  показан на рис. 15.22.
показан на рис. 15.22.
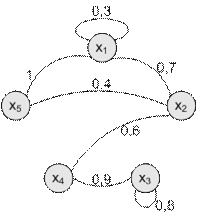
Рис. 1522. Нечеткий граф 
Пример 7. Записать матрицу смежности нечеткого неориентированного графа  = (X,
= (X,  ), заданного в примере 1.
), заданного в примере 1.
Решение: Матрица смежности R x 1 нечеткого неориентированного графа  , рассмотренного в примере 1, запишется следующим образом:
, рассмотренного в примере 1, запишется следующим образом:
| x 1 | x 2 | x 3 | x 4 | x 5 | |||
| R x 1 = | x 1 | 0,3 | 0,7 | . | |||
| x 2 | 0,7 | 0,6 | 0,4 | ||||
| x 3 | 0,8 | 0,9 | |||||
| x 4 | 0,6 | 0.9 | |||||
| x 5 | 0,4 |
Пример 8. Записать нечеткий неориентированный граф второго вида.
Решение: Зададим нечеткий неорграф второго вида  = (
= ( ,
,  ), у которого
), у которого  = {<1/ x 1>,<0,4/ x 2>,<0,7/ х 3>,<0,5/ x 4>, <0,9/ х 5>},
= {<1/ x 1>,<0,4/ x 2>,<0,7/ х 3>,<0,5/ x 4>, <0,9/ х 5>},  = {<0,3/(х 1, х 1)>, <0,7/(х 1, х 2)>, <1/(х 1, х 5)>, <0,6/(х 2, х 4)>.<0,4/(х 2, х 5)>, <0,9/(х 3, х 4)>, <0,8/(х 3, х 3)>}.
= {<0,3/(х 1, х 1)>, <0,7/(х 1, х 2)>, <1/(х 1, х 5)>, <0,6/(х 2, х 4)>.<0,4/(х 2, х 5)>, <0,9/(х 3, х 4)>, <0,8/(х 3, х 3)>}.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что такое граф? Приведите пример. Назовите известные вам типы графов.
2. В чем состоит различие между ориентированными и неориентированными графами?
3. Опишите известные вам способы задания графов.
4. Что называется подграфом и суграфом графа?
5. Что называется дополнением графа?
6. Какой граф называется двойственным?
7. Какие операции могут выполняться над графами?
8. Что такое мультиграф и как определяется его мультичисло?
9. Дайте определение регулярного графа.
10. Дайте определение нечеткого графа. В чем состоит отличие нечеткого неориентированного графа первого и второго рода?
Дата добавления: 2015-10-26; просмотров: 286 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Способы задания графов | | | Маршруты, цепи, циклы |