Эйлеровы и гамильтоновы цепи и циклы

При решении задач информатики важное значение имеют графы специального вида ─ Эйлеровы и Гамильтоновы.

Постановка задачи о Кенигсберских мостах знаменует начало создания теории графов. На рис. 16.1 показан условный план города, а на рис. 16.2 ─ его модель в виде графа. Здесь A, B, C, D (рис. 16.1) ─ суша, a, b, c, d, e, f, g – мосты, соединяющие сушу между собой.

Рис. 16.1. Условный план города

Рис. 16.2. Модель плана города в виде графа

Требуется пройти каждый мост по одному разу и вернуться в исходную часть города. На рис. 2.2 вершины графа ─ части города, а ребра графа ─ мосты.

Все вершины графа на рис. 2.2 имеют нечетную степень, следовательно, решения нет.

Теорема 16.1 (Л. Эйлер 1736 г.) Связный неориентированный граф содержит эйлеров цикл (эйлерову цепь) тогда и только тогда, когда число вершин нечетной степени равно 0 (или 2).

Доказательство для цикла:

1) Необходимость: Любой Эйлеров цикл (ЭЦ) должен прийти в вершину по одному ребру и покинуть ее по другому, так как любое ребро должно использоваться только один раз. Поэтому, если G содержит ЭЦ, то степени всех вершин должны быть четными.

2) Достаточность: Пусть G ─ связный неорграф, все вершины которого имеют четную степень. Начнем путь из произвольной вершины x ₀ и пойдем по некоторому ранее не использованному ребру к следующей вершине и так до тех пор, пока не вернемся в x ₀ и не замкнем цикл. Если все ребра использованы, то ЭЦ построен. Если некоторые ребра не использованы, то процесс продолжается. Пусть Ф ─ построенный цикл (рис. 2.3) и Ф1 ─ цикл с не использованными ребрами.

Рис. 16.3. Пример построения эйлерова цикла

Так как G связен, то Ф должен проходить через вершину, являющуюся концом неиспользованного ребра.

Если удалить ребра Ф, то в оставшемся графе вершины по-прежнему будут иметь четную степень, так как в Ф должно быть четное число ребер, инцидентных каждой вершине. Начиная с x_i, получаем цикл Ф1. Если все ребра использованы, то ЭЦ построен путем Ф È Ф1. Если остались неиспользованные ребра, то процесс снова продолжается, до тех пор, пока не будут использованы все ребра и построен ЭЦ Ф (рис. 16.4). Это доказывает теорему.

Рис. 16.4. Пример эйлерова цикла в графе

Граф называется полуэйлеровым, если существует незамкнутая цепь, проходящая через каждое ребро графа только один раз. Конечный граф G является эйлеровым, если он связен и все его локальные степени четны. Если эйлеров цикл Сэ существует, то, проходя по его ребрам, можно нарисовать эйлеров граф на бумаге, не отрывая карандаша. На рис. 16.5 ─ 16.7 показаны неэйлеров (рис. 16.5), полуэйлеров (рис 16.6) и эйлеров (16.7) графы. Порядок обхода полуэйлерова и эйлерова графов показан стрелками.

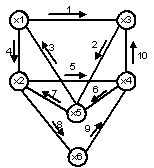
Рис. 16.5. Неэйлеров граф Рис. 16.6. Полуэйлеров граф

Рис. 16.7. Эйлеров граф

Например, граф G (рис. 16.6) не является эйлеровым, так как степени вершин x ₁, x ₃ ─ нечетны. Граф G также не является эйлеровым, если он не связен, хотя его компоненты могут являться эйлеровыми графами.

Заметим, что связный граф G является полуэйлеровым, когда в нем не более двух вершин имеют нечетные локальные степени. Причем одна из этих вершин будет начальной, а другая конечной.

Запишем алгоритм Флери построения Сэ в связном графе G = (X, U), локальные степени которого четны.

1°. Пусть начальная вершина цикла x_k = x ₁. Число ребер U графа G равно |U| = n, а x_s – произвольно выбранная вершина графа. Эйлеров цикл Ci = Æ.

2°. Определяем множество ребер, смежных вершине x_s.

3°. Выбираем ребро, удаление которого не приведет к разбиению графа на два компонента связности (кроме изолированных вершин). Пусть это будет ребро u_k = (x_s, x_p).

4°. Тогда добавляем это ребро в эйлеров цикл C_k = C_k È u_k и удаляем его из графа G.

5°. Если выполняется условие | C_k | = n, то переход к п. 7°, иначе переход к п. 6°.

6°. Присваиваем k = k + 1, s = p и переходим к п. 2°.

7°. Эйлеров цикл построен, конец работы алгоритма.

Также можно привести еще один вариант записи алгоритма Флери.

1°. Выбирается произвольная вершина x_i, i Î I = {1, 2,..., n}.

2°. Определяется произвольное ребро (x_i, x_j) j ¹ i, j Î I, инцидентное вершине x_i, ему присваивается номер 1. Это ребро заносится в список Lэ и вычеркивается из графа G.

3°. Рассматривается вершина x_j, если есть возможность другого выбора, не выбираются ребра (x_j, x_k), ему присваивается номер, оно заносится в список Lэ и вычеркивается из G.

4°. Производится проверка |Lэ| = m. Если да, то переход к п. 5°, если нет, то п. 3° повторяется для вершин x_b,..., x_n.

5°. Построен эйлеров цикл Сэ, конец работы алгоритма.

На рис. 16.7 стрелками показан пример работы алгоритма

Сэ = (x ₁, x ₂), (x ₂, x ₆), (x ₆, x ₃), (x ₃, x ₂), (x ₂, x ₄), (x ₄, x ₅), (x ₅, x ₃), (x ₃, x ₁).

Цикл, проходящий по всем вершинам графа G один раз, называется гамильтоновым, а G называется гамильтоновым графом. Например, граф G (рис. 16.7) не имеет гамильтонова цикла (ГЦ), а граф G (рис. 16.5) имеет Gг = (x ₁, x ₂), (x ₂, x ₅), (x ₅, x ₄), (x ₄, x ₃), (x ₃, x ₁). В отличие от эйлеровых циклов для ГЦ неизвестен общий критерий существования. В основном известны только теоремы, дающие достаточные условия существования ГЦ.

Теорема 16.2. Если в графе G с n вершинами для любой пары несмежных вершин x_i, x_j верно: r (x_i) + r (x_j) ³ n, то G имеет ГЦ.

Из теоремы следует результат Дирака, что граф имеет ГЦ, если для каждой его вершины

r (x_i) ³ n/2. (16.1)

Дата добавления: 2015-10-26