Примеры решения задач. Пример 1. Пусть задан граф G, показанный на рис

Пример 1. Пусть задан граф G, показанный на рис. 15.23. Подсчитать количество маршрутов длиной 3 в данном графе.

Решение: Запишем матрицу смежности графа G:

.

Как уже было показано ранее, чтобы найти число маршрутов длиной 2, в заданном графе необходимо возвести его матрицу смежности в квадрат. Алгебраическое произведение матриц определяется по формуле

r ² _ij = 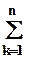a_ik b_ki,

где r ² _ij ─ элемент матрицы R².

Вычислив, таким образом, значения всех элементов, мы придем в итоге к следующей матрице:

.

Для того, чтобы определить количество маршрутов длиной 3 в исходном графе, необходимо полученную на первом шаге матрицу R² умножить на R. Например,

r ³_1,2 = r _1,1 r ²_1,2 + r _1,2 r ²_2,2 + r _1,3 r ²_3,2 + r _1,4 r ²_4,2 = 0*0 + 1*2 + 2*3 + 0*0 = 4.

Используя вышеуказанную формулу умножения матриц, получим:

.

Из полученной матрицы R³ следует, что в исходном графе между вершинами, например, x ₁ и x ₂, существует 4 маршрута длиной 3: S₁ = (x ₁, x ₂)(x ₂, x ₁)(x ₁, x ₂); S₂ = (x ₁, x ₂)(x ₂, x ₄)(x ₄, x ₂); S₃ = (x ₁, x ₃)(x ₃, x ₁)(x ₁, x ₂); S₄ = (x ₁, x ₃)(x ₃, x ₄)(x ₄, x ₂).

Пример 2. Для графа, изображенного на рис. 15.29, привести примеры маршрута, цепи, цикла, простой цепи и простого цикла.

Рис. 15.29. Пример графа G

Ответ: Маршрутом в графе является любая конечная последовательность ребер, причем маршрут может проходить через одну и ту же вершину или ребро любое число раз. Тогда в качестве маршрута можно принять такую конечную последовательность: S = (x ₁, x ₂), (x ₂, x ₆), (x ₆ ─ x ₂), (x ₂ ─ x ₇), (x ₇ ─ x ₆), (x ₆ ─ x ₂). Цепью называют маршрут, не имеющий повторяющихся ребер. Таким образом, последовательность S = (x ₁, x ₂), (x ₂, x ₄), (x ₄, x ₆), (x ₆, x ₂), (x ₂, x ₇) можно считать цепью. Цикл представляет собой замкнутую цепь, т. е. цепь, у которой первая и последняя вершины совпадают. Тогда последовательность C = (x ₁, x ₅), (x ₅, x ₃), (x ₃, x ₁), (x ₁, x ₈), (x ₈, x ₅), (x ₅, x ₁) является циклом. При это, как мы видим, цепь и цикл могут проходить несколько раз через одну и ту же вершину. Простая цепь (цикл) не может включать в себя ни повторяющихся ребер, ни вершин. Примером простой цепи может служить последовательность S = (x ₁, x ₂), (x ₂, x ₄), (x ₄, x ₆), (x ₆, x ₈), (x ₈, x ₃); а простой цикл C = (x ₁, x ₅), (x ₅, x ₃), (x ₃, x ₁).

Пример 3. Для графа, заданного на рис. 15.30 привести пример разреза, правильного разреза.

Ответ: Правильными разрезами будут: U₁ = {(x ₃, x ₆), (x ₄, x ₆), (x ₄, x ₇); U₂ = {(x ₄, x ₁₀), (x ₅, x ₁₀)}; U₃ = {(x ₅, x ₁₂)}; U₄ = {(x ₅, x ₁₅)}. А разрез U определяется как их объединение: U = U₁ È U₂ È U₃ È U₄.

Рис. 15.30. Пример графа G

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Что из себя представляет маршрут в графе?

2. Как определяется длина маршрута?

3. Что такое маршрут в графе. Как определяется длина маршрута?

4. Дайте определение цепи, цикла, простого цикла и простой цепи в графе.

5. Какой граф называется связным?

6. Что такое компонента связности?

7. Что такое блок графа?

8. Дайте определение разреза, правильного разреза графа. Приведите примеры.

9. Дайте определение вершинной связности. Приведите примеры.

10. Дайте определение реберной связности. Приведите примеры.

Дата добавления: 2015-10-26