
Читайте также:
|
Пример 1. Привести примеры графов:
а) содержащих одновременно ЭЦ и ГЦ,
б) содержащих ГЦ и не содержащих ЭЦ,
в) содержащих ЭЦ и не содержащих ГЦ,
г) не содержащих ни ЭЦ и ГЦ.
На рис. 16.17 приведены примеры графов, соответствующих заданным в данном примере условиям. Для эйлеровых графов на рисунке стрелками показан порядок обхода ребер графа.

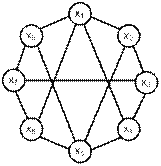
а б
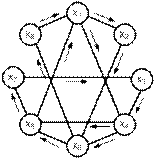
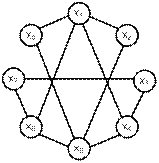
в г
Рис. 16.17. Примеры эйлеровых и гамильтоновых графов
Пример 2. Для графа G = (X, U), заданного на рис. 16.17,в, построить ЭЦ, используя алгоритм Флери.
Решение: Из рисунка 16.17,в видно, что граф G ─ связный, поэтому переходим к алгоритму построения ЭЦ в графе.
1.1. Производим подсчет локальных степеней графа G. Все вершины имеют четные степени. Переходим к п. 1.2.
1.2. Выбираем вершину x 1.
1.3. Выбираем ребро u (x 1 – x 4). Здесь и далее в алгоритме примем следующее обозначение: u (x 1 – x 4) = u 14. Заносим его в список L и вычеркиваем из матрицы смежности R.
1.4. |L| ¹ m, где m ─ число ребер в графе G, переходим к п. 1.5.
1.5. Переходим к вершине x 4.
2.3. Выбираем ребро u 45.Заносим его в список L и вычеркиваем из матрицы смежности.
2.4. |L| ¹ m, переходим к п. 2.5.
2.5. Переходим к вершине x 5.
3.3. Выбираем ребро u 56 и заносим его в список L.
3.4. |L| ¹ m, переходим к п. 3.5.
3.5. Переходим к вершине x 6.
4.3. Выбираем ребро u 67 (ребро u 61 не выбираем, поскольку в данный момент имеется возможность выбрать другое ребро).
4.4. |L| ¹ m, переходим к п. 4.5.
4.5. Переходим к вершине x 7.
5.3. Выбираем ребро u 73. Заносим его в список L.
5.4. |L| ¹ m, переходим к п. 5.5.
5.5. Выбираем вершину x 3.
6.3. Выбираем ребро u 34, и заносим его в список L.
6.4. |L| ¹ m, переходим к п. 6.5.
6.5. Выбираем вершину x 4.
7.3. Выбираем ребро u 46, заносим его в список L.
7.4. |L| ¹ m, переходим к п. 7.5.
7.5. Выбираем вершину x 6.
8.3. Поскольку иных вариантов нет, выбираем ребро u 61.
8.4. |L| ¹ m, переходим к п. 8.5.
8.5. Выбираем вершину x 1.
9.3. Выбираем ребро u 12, заносим его в список L.
9.4. |L| ¹ m, переходим к п. 9.5.
9.5. Выбираем вершину x 2.
10.3. Выбираем ребро u 25, заносим его в список L.
10.4. |L| ¹ m, переходим к п. 10.5.
10.5. Выбираем вершину x 5.
11.3. Выбираем ребро u 58, заносим его в список L.
11.4. |L| ¹ m, переходим к п. 11.5.
11.5. Выбираем вершину x 8.
12.3. Выбираем ребро u 81, заносим его в список L.
12.4. |L| = m, переходим к п. 12.6.
12.6. Построен ЭЦ (u 14 – u 45 – u 56 – u 67 – u 73 – u 34 - u 46 – u 61 – u 12 – u 25 – u 58 – u 81).
Поставленная задача выполнена. Работа алгоритма закончена.
Пример 3. Привести пример гамильтонова графа и показать на нем порядок обхода вершин.
Решение: На рис. 16.18 показан граф G, в котором имеется гамильтонов цикл. Ребра, входящие в гамильтонов цикл, выделены жирной линией. Последовательность обхода вершин графа в гамильтоновом цикле может быть следующей: ГЦ = (x 1 ─ x 2 ─ x 15 ─ x 13 ─ x 18 ─ x 16 ─ x 14 ─ x 6 ─ x 7 ─ x 17 ─ x 20 ─ x 19 ─ x 11 ─ x 12 ─ x 3 ─ x 4 ─ x 10 ─ x 9 ─ x 8 ─ x 5 ─ x 1).

Рис. 16.18. Пример гамильтонова цикла в графе
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Какой цикл в графе называется эйлеровым? Что такое полуэйлеров граф?
2. Какие условия существования эйлерова цикла в графе?
3. Что такое гамильтонов цикл в графе?
4. Существуют ли условия, позволяющие однозначно определить наличие гамильтонова цикла в произвольном связном графе?
5. В чем заключается основная идея алгоритма Флери?
6. Что такое граф подразбиений?
7. Какой граф называется тотальным?
8. В каком случае ребра и вершины графа называются соседними?
9. Поясните понятие жордановой кривой?
10. Что такое замкнутая жорданова кривая?
Дата добавления: 2015-10-26; просмотров: 168 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Связь между эйлеровыми и гамильтоновыми графами | | | Алгоритм Робертса ─ Флореса |