Алгоритм Робертса ─ Флореса

Рассмотрим алгоритм Робертса и Флореса для построения гамильтонова цикла на графе. Алгоритм основан на переборе вершин, входящих в анализируемые цепи. Рассматриваемая цепь непрерывно продлевается до момента, когда построен гамильтонов цикл или если эта цепь не приводит к его построению. Тогда рассматривается другая цепь, и процесс продолжается сначала, пока не будет найден гамильтонов цикл или будут рассмотрены все цепи и окажется, что этот цикл не найден.

Исходной информацией является специальная матрица M = | m_ij | _{k × n}. Здесь k ─ это параметр, определяющий число строк матрицы. Величина m_ij определяет метку первой вершины, для которой есть ребро u_i,j. Число строк матрицы равно наибольшей локальной степени в анализируемом графе. Например, задан граф G (рис. 16.19) и его матрица.

		a	b	c	d	e	f
		b	a	a	c	b	a
М =		c	c	b	e	c	b
		f	e	d	–	d	c	.
		–	f	e	–	–
		–	–	f	–	–

.

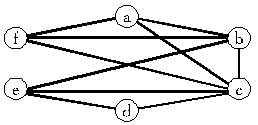
Рис. 16.19. Граф G

Рассмотрим работу алгоритма на примере. Алгоритм начинается с рассмотрения элементов первого столбца матрицы М, если не задана иная начальная вершина гамильтонова цикла.

1.1. Выбираем вершину a. В списке вершин графа G, смежных с вершиной a (столбец a матрицы М), первой стоит вершина b.

1.2. Заносим в последовательность обхода вершин вершину b:

ГЦ = [ a ─ b ], переходим к столбцу b матрицы M.

1.3. Так как гамильтонов цикл еще не построен, продолжаем вычисления.

2.1. В списке вершин графа G, смежных с вершиной b, первой стоит вершина a, однако она уже задействована в цикле. Поэтому выбираем следующую вершину в столбце. Это вершина c.

2.2. Заносим в последовательность обхода вершин вершину c:

ГЦ = [ a ─ b ─ c ], переходим к столбцу c матрицы M.

2.3. Гамильтонов цикл еще не построен, продолжаем вычисления.

3.1. В списке вершин графа G, смежных с вершиной c, вершины a и b мы пропускаем, так как они использованы в цикле. Выбираем вершину d.

3.2. Заносим в последовательность обхода вершин вершину d:

ГЦ = [ a ─ b ─ c ─ d ], переходим к столбцу d матрицы M.

3.3. Гамильтонов цикл еще не построен, продолжаем вычисления.

4.1. В списке вершин графа G, смежных с вершиной d, пропускаем вершину c и выбираем вершину e.

4.2. Заносим в последовательность обхода вершин вершину e:

ГЦ = [ a ─ b ─ c ─ d ─ e ], переходим к столбцу e матрицы M.

4.3. Гамильтонов цикл еще не построен, продолжаем вычисления.

5.1. В списке вершин графа G, смежных с вершиной e, все вершины уже задействованы в цикле.

5.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b - c ─ d ].

6.1. В списке вершин графа G, смежных с вершиной d, все вершины уже задействованы в цикле.

6.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b ─ c ].

7.1. В списке вершин графа G, смежных с вершиной c, пропускаем вершину d и выбираем вершину e.

7.2. Заносим в последовательность обхода вершин вершину e:

ГЦ = [ a ─ b ─ c ─ e ], переходим к столбцу e матрицы M.

7.3. Гамильтонов цикл еще не построен, продолжаем вычисления.

8.1. В списке вершин графа G, смежных с вершиной e, пропускаем вершины b и c, после чего выбираем вершину d.

8.2. Заносим в последовательность обхода вершин вершину d:

ГЦ = [ a ─ b ─ c ─ e ─ d ], переходим к столбцу d матрицы M.

8.3. Гамильтонов цикл еще не построен, продолжаем вычисления.

9.1. В списке вершин графа G, смежных с вершиной d, все вершины уже задействованы в цикле.

9.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b ─ c ─ e ].

10.1. В списке вершин графа G, смежных с вершиной e, все вершины уже задействованы в цикле.

10.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b ─ c ].

11.1. В списке вершин графа G, смежных с вершиной c, пропускаем вершину e и выбираем вершину f.

11.2. Заносим в последовательность обхода вершин вершину f:

ГЦ = [ a ─ b ─ c ─ f ], переходим к столбцу f матрицы M.

11.3. Гамильтонов цикл еще не построен, продолжаем вычисления.

12.1. В списке вершин графа G, смежных с вершиной f, все вершины уже задействованы в цикле.

12.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a - b - c ].

13.1. В списке вершин графа G, смежных с вершиной c, все вершины уже задействованы в цикле.

13.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a - b ].

14.1. В списке вершин графа G, смежных с вершиной b, пропускаем вершину c и выбираем вершину e.

14.2. Заносим в последовательность обхода вершин вершину e:

ГЦ = [ a ─ b ─ e ], переходим к столбцу c матрицы M.

14.3. Гамильтонов цикл еще не построен, продолжаем вычисления.

15.1. В списке вершин графа G, смежных с вершиной e, пропускаем вершину b и выбираем вершину c.

15.2. Заносим в последовательность обхода вершин вершину c:

ГЦ = [ a ─ b ─ e ─ c ], переходим к столбцу c матрицы M.

15.3. Гамильтонов цикл еще не построен, продолжаем вычисления.

16.1. В списке вершин графа G, смежных с вершиной c, выбираем вершину d.

16.2. Заносим в последовательность обхода вершин вершину d:

ГЦ = [ a ─ b ─ e ─ c ─ d ], переходим к столбцу d матрицы M.

16.3. Гамильтонов цикл еще не построен, продолжаем вычисления.

17.1. В списке вершин графа G, смежных с вершиной d, все вершины уже задействованы в цикле.

17.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b ─ e ─ c ].

18.1. В списке вершин графа G, смежных с вершиной c, выбираем вершину f.

18.2. Заносим в последовательность обхода вершин вершину f:

ГЦ = [ a ─ b ─ e ─ c ─ f ], переходим к столбцу f матрицы M.

18.3. Гамильтонов цикл еще не построен, продолжаем вычисления.

19.1. В списке вершин графа G, смежных с вершиной f, все вершины уже задействованы в цикле.

19.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b ─ e ─ c ].

20.1. В списке вершин графа G, смежных с вершиной c, все вершины уже задействованы в цикле.

20.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b ─ e ].

21.1. В списке вершин графа G, смежных с вершиной e, пропускаем вершину c и выбираем вершину d.

21.2. Заносим в последовательность обхода вершин вершину d:

ГЦ = [ a ─ b ─ e ─ d ], переходим к столбцу c матрицы M.

21.3. Гамильтонов цикл еще не построен, продолжаем вычисления.

22.1. В списке вершин графа G, смежных с вершиной d, выбираем вершину c.

22.2. Заносим в последовательность обхода вершин вершину c:

ГЦ = [ a ─ b ─ e ─ d ─ c ], переходим к столбцу c матрицы M.

22.3. Гамильтонов цикл еще не построен, продолжаем вычисления.

23.1. В списке вершин графа G, смежных с вершиной c, выбираем вершину f.

23.2. Заносим в последовательность обхода вершин вершину f:

ГЦ = [ a ─ b ─ e ─ d ─ c ─ f ], переходим к столбцу c матрицы M.

23.3. Гамильтонов цикл еще не построен, продолжаем вычисления.

24.1. В списке вершин графа G, смежных с вершиной f, выбираем вершину a, поскольку это завершающее ребро гамильтонова цикла.

23.2. Заносим в последовательность обхода вершин вершину a:

ГЦ = [ a ─ b ─ e ─ d ─ c ─ f ─ a ].

23.3. Гамильтонов цикл построен, работа алгоритма завершена.

Главное преимущество алгоритма ─ простота, а его основным недостатком является сложность в случае необходимости перебора всех путей в процессе построения гамильтонова цикла. В случае же, когда гамильтонова цикла в графе не существует, алгоритм и вовсе сведется к полному перебору всех возможных вариантов построения пути.

Если в графе можно построить несколько гамильтоновых циклов, то алгоритм позволяет последовательно определить все гамильтоновы циклы. Кроме того, алгоритм позволяет определять и гамильтоновы цепи.

Дата добавления: 2015-10-26