Расстояния на графах

Рассмотрим метрику графов. Метрика графа основана на понятии расстояния. Расстоянием d (x_i, x_j), между вершинами x_i, x_j Î X графа G = (X, U) называется длина кратчайшей цепи, соединяющей эти вершины. Под длиной цепи понимается число входящих в нее ребер. Функция d (x_i, x_j), определенная на множестве ребер графа G, называется метрикой графа.

Функцию расстояний для графа G удобно задавать матрицей расстояний D = || d_{i , j} || _{n × n} или ее списком. Элемент матрицы определяется следующим образом:

d_{i , j} = . (16.5)

Например, для графа G (рис. 16.26)

Рис. 16.26. Граф G

матрица расстояний имеет вид

D=							.

Список расстояний можно записать в виде множества, состоящего из кортежей длины три:

L_D = {<1, 2, 1>, <1, 3, 1>, <1, 4, 2>, <1, 5, 1>, <2, 3, 2>, <2, 4, 1>, <2, 5, 1>, <3, 4, 1>, <3, 5, 1>, <4, 5, 1>}.

Первый элемент в кортеже соответствует вершине x_i графа, второй элемент – вершине x_j, а третий элемент кортежа – расстоянию d_{i , j}.

Если известны расстояния между любой парой вершин графа, то можно определить его диаметр d (G) как максимальное расстояние между его вершинами:

d (G) = max d_{i , j} , i, j Î I = {1, 2,..., n}. (16.6)

Кратчайшие простые цепи, связывающие вершины i, j Î X с максимальным расстоянием между ними, называются диаметрально простыми цепями.

Пусть v – произвольная вершина G = (X, U). Максимальным удалением в графе G от вершины v называется величина:

r (v) = max d_v,x, v, x Î X. (16.7)

Согласно Ф. Харари эксцентриситет вершины v в связном графе G определяется как max d_v,x, v, x Î X по всем вершинам x.

Тогда радиусом графа r (G) называется наименьший из эксцентриситетов вершин. Любая кратчайшая цепь от центра v до максимально удаленной от него вершины x – радиальной цепью.

R(G) = min r (x), x Î X. (16.8)

Вершина v называется центром графа, если среди всех вершин с максимальным удалением от нее выбирается удаление, принимающее минимальное значение.

Центр не обязательно должен быть единственным. Например, в полном графе K_n, радиус равен 1 и любая вершина является центром.

Пусть G – конечный граф G = (X, U), |U| = m. Количество последовательностей ребер этого графа без повторений конечно и равно m!. Тогда конечно и число простых цепей, в которых ребра не повторяются. Протяженностью g (v’, v’’) между вершинами v’, v’’ Î X называется максимальная из длин, связывающих эти вершины.

Если исключить из этих простых цепей циклы, то для любой вершины v Î X, g (v, v) = 0. В этом случае протяженность также удовлетворяет аксиомам метрики.

Пусть L(v’, v’’’) – самая длинная простая цепь, соединяющая вершины v’ – v’’’. Пусть L*(v’’, v’) – некоторая простая цепь, соединяющая вершины v’’ и v’. Пусть 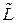(v’’, v ⁴) – участок последней цепи до первого пересечения с L.

Тогда v⁴ делит цепь на 2 участка L’, L’’. Участки L’ и 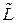составляют простую цепь с началом v’ и концом v’’, а L’’ и 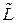– простую цепь, соединяющую v’’ и v’’’, причем сумма их длин не меньше длины цепи L. Значит и сумма максимальных длин путей с теми же началами и концами равная g (v’, v’’) + g (v’’, v’’’) не меньше длины цепи L, которая равна g (v’, v’’’) (рис 16.27).

В графе G существуют диаметральные по протяженности или длиннейшие простые цепи. Их длина l ₀ называется диаметром протяженности. Для каждой вершины v существуют самые длинные простые цепи с концами в этой вершине. Их длина g (v) = max g (v, v’), v’ Î v называется числом протяженности для вершины v.

Рис. 16.27. Длины простых цепей

Для логических задач представляет интерес нахождение функции расстояний для графов G _r частного вида, называемых координатной решеткой. В графе G _r = (X _r, U _r) множество вершин X _r соответствует узлам решетки (сетки), а множество ребер U _r горизонтальным и вертикальным отрезкам, соединяющим узлы решетки. Пример графа G _r, т.е. координатной решетки, показан на рис. 16.28. Расстояние между двумя смежными вершинами в G _r, называемое шагом решетки, будем считать равным единице.

Рис. 16.28. Пример координатной решетки G _r

Расстояние d_{i , j} между двумя произвольными вершинами в G _r можно определить по формуле

d_{i , j} = | s_i – s_j | + | t_i – t_j |, (16.9)

где s_i, s_j и t_i, t_j — координаты вершин x_i, x_j Î X. Обычно задаются размеры решетки p × q, где p — число узлов решетки по оси s, а q — по оси t.

Например, для графа G _r (рис. 16.28) расстояние

d _6,10 = | s ₆ – s ₁₀| + | t ₆ – t ₁₀| = |0 – 2| + |1 – 3| = 4,

т.е. из вершины x ₆ необходимо пройти четыре ребра G _r, чтобы попасть в вершину x ₁₀.

Если произвольный граф G отображается в G _r так, что любые вершины G размещаются в узлах решетки, то расстояние между вершинами G определяется как расстояние между соответствующими узлами решетки. Если расстояние d_{i , j} определять как длину кратчайшей прямой, соединяющей вершины x_i, x_j, то

d_{i , j} = (16.10)

Заметим, что первый способ определения d_{i , j} проще, так как при этом d_{i , j} принимает только целочисленные значения. Любой граф G может быть отображен в решетку G _r. Для подсчета суммарной длины L(G) ребер графа G = (X, U), отображенного в решетку G _r, введем понятие матрицы геометрии D(g).

Матрица геометрии D(g) представляет собой часть матрицы расстояний D, в которой исключены элементы d_{i , j}, если вершины x_i, x_j Î X не смежны в графе G. Для построения матрицы геометрии D(g) графа G необходимо каждый элемент матрицы D умножить на соответствующий элемент матрицы смежности R: D(g) = || r_i,j, d_{i , j} || _{n × n}.

Например, граф G без учета весов ребер отобразим в решетку G _r размера 3×2 (рис. 16.29).

Рис 16.29. Пример графа, отображенного в решетку

Матрицы R и D графа G примут вид:

R = 3

, D = 3

.

Тогда можно определить матрицу геометрии D(g) = R × D:

							r (xi)
								.
D(g) = 3

Сумма элементов матрицы D(g) определяет удвоенную суммарную длину ребер графа G при данном отображении его в решетку G _r. Для рассмотренного примера суммарная длина ребер графа L(G) составляет 13 условных единиц. При другом отображении графа в решетку суммарная длина L(G) изменяется, хотя в частном случае может совпадать с предыдущим значением.

Дата добавления: 2015-10-26