Примеры решения задач. Пример 1. Пусть задан граф g = (x, u), изображенный на рис

Пример 1. Пусть задан граф G = (X, U), изображенный на рис. 16.41,а. Привести примеры произвольного и покрывающего деревьев для заданного графа.

Ответ: Пример покрывающего дерева приведен на рис. 16.41,б. На 16.41,в,г приведены примеры выделения произвольных деревьев из исходного графа.

а исходный граф б покрывающее дерево

в произвольное дерево г произвольное дерево

Рис. 16.41. Граф G и его деревья: а – исходный граф; б – покрывающее дерево; в – произвольное дерево; г – произвольное дерево.

Пример 2. Записать все покрывающие деревья для полного графа на три вершины, заданного на рис. 16.42,а.

Решение: согласно теореме Кэли число покрывающих деревьев полного графа равно: t = n ^{n - 2}.

Таким образом, подставив в формулу число вершин заданного графа, получим результат t = 3 ^{3 - 2} =3¹ = 3.

Из полученного результата следует, что для данного графа можно построить три покрывающих дерева как это показано на рис. 16.42,б.

а б

Рис. 16.42. Граф (а) и множество его покрывающих деревьев(б)

Пример 3. Пусть задан граф G = (X, U), изображенный на рис. 16.43,а. Построить кратчайшее покрывающее дерево (КПД), используя алгоритм Краскала.

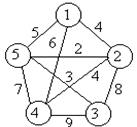
Рис. 16.43. а Граф G

Решение: запишем треугольную матрицу смежности R заданного графа.

R =							.

1.1. Выбираем по матрице смежности минимальный элемент. Это ребро u ₂₅. Заносим его в массив M = { u ₂₅}.

1.2. Выбранное ребро единственное, поэтому переходим к пункту 3.

1.3. |M| ¹ n - 1, переходим к пункту 1.

2.1. Выбираем ребро u ₃₅, заносим его в массив M = { u ₂₅, u ₃₅}.

2.2. Цикл не образуется, поскольку в массиве всего два ребра.

2.3. |M| ¹ n - 1, переход к пункту 1.

3.1. Выбираем ребро u ₁₂, заносим его в список M = { u ₂₅, u _35, u ₁₂}.

3.2. Проверяем выбранные ребра. Цикл не образуется, поэтому переходим к пункту 3.

3.3. |M| ¹ n - 1, переходим к пункту 1.

4.1. Выбираем ребро u ₂₄, заносим его в список M = { u ₂₅, u _35, u _12, u ₂₄}.

4.2. Проверяем выбранные ребра. Цикл не образуется, поэтому переходим к пункту 3.

4.3. Мощность |M| = 4. Так как 4 = 5 – 1, алгоритм закончен. Кратчайшее покрывающее дерево (КПД) построено (рис. 16.43,б). Его суммарный вес равен S_КПД = 2 + 3 + 4 + 4 = 13.

б

Рис. 16.43. (б) Кратчайшее покрывающее дерево для графа G (рис. 6.43 а)

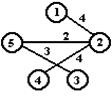
Пример 4. Построить КПД для графа G, изображенного на рис. 16.44, используя алгоритм Прима.

Рис. 16.44. Исходный граф

Решение

1.1. Выбираем произвольную вершину. Пусть это будет вершина x ₁. Составляем список:

1.2. Из списка L₁ выбираем ребро (1, 2) и включаем его в поддерево T’ =

={(1, 2)}.

1.3. Так как цикл не образуется, переходим к пункту 4.

1.4. Как видно |X’| ¹ |X|, следовательно, переходим к пункту 5.

1.5. Добавляем в список L₁ ребра, инцидентные вершине x ₂ и после переупорядочивания списка L₁ получаем новый список L₂.

.

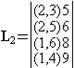2.2. Выбираем из списка L₂ ребро (2, 3) и включаем его в поддерево T’ = {(1, 2); (2, 3)}.

2.3. Цикл не образуется, переход к пункту 4.

2.4. |X’| ¹ |X|, переходим к пункту 5.

2.5. Добавляем в список L ребра, инцидентные вершине x _3, и переупорядочиваем список. Переходим к пункту 2.

.

3.2. Из списка L₃ выбираем ребро (3, 4) и заносим его в поддерево T’ = {(1, 2); (2, 3); (3, 4)}.

3.3. Цикл не образуется, переходим к пункту 4.

3.4. |X’| ¹ |X|, переходим к пункту 5.

3.5. Добавляем в список L ребра, инцидентные вершине x ₄, и переупорядочиваем список. Ребро (1, 4) исключено из списка L_4, так как оно образует цикл с уже выбранными ребрами. Переходим к пункту 2.

.

4.2. Из списка L₄ выбираем ребро (4, 5) и включаем его в поддерево T’ = {(1, 2); (2, 3); (3, 4); (4, 5)}.

4.3. Цикл не образуется, переходим к пункту 4.

4.4. | X’| ¹ |X|, переходим к пункту 5.

4.5. Добавляем в список L ребра, инцидентные вершине x ₅, и переупорядочиваем список. Ребро (2, 5) исключено из списка L₅, т.к. оно образует цикл с уже выбранными ранее ребрами. Переходим к пункту 2.

.

5.2. Из списка L₅ выбираем ребро (3, 6) и включаем его в поддерево T’ = {(1, 2); (2, 3); (3, 4); (4, 5); (3, 6)}.

5.3. Цикл не образуется, переход к пункту 4.

5.4. |X’| = |X|, переход к пункту 6.

5.6. Построено КПД (рис. 16.45): T’ = {(1, 2); (2, 3); (3, 4); (4, 5); (3, 6)} c суммарным весом равным S_КПД = 2 + 5 + 1 + 3 + 4 = 15.

Работа алгоритма закончена.

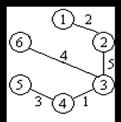
Рис. 16.45. Кратчайшее покрывающее дерево

Пример 5. Для графа G _r, заданного на рис. 16.46, построить кратчайшее покрывающее дерево.

Рис. 16.46. Задача построения дерева Штейнера

Решение: подсчитаем разность координат по обеим осям:

ось s: 10 - 1 = 9,

ось t: 9 - 2 = 7.

Перепад координат по оси t меньше, следовательно, проводим перпендикуляр к оси t.

Теперь определим точку, через которую мы проведем ось дерева. Поскольку число вершин слева и справа от предполагаемой оси равно, проводим перпендикуляр, к примеру, через точку с координатой t = 6. Таким образом, мы провели ось дерева Штейнера.

И теперь, соединив с полученной осью все вершины графа, не находящиеся на оси, мы получим в итоге дерево Штейнера (рис. 16.47). Суммарная длина дерева Штейнера находится путём простого сложения длин отрезков составляющих дерево:

L_å = 1 + 2 + 1 + 2 + 4 + 3 + 3 + 9 = 25.

Рис. 16.47. Дерево Штейнера

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Приведите механизмы определения деревьев в произвольном графе.

2. Приведите определение произвольного, покрывающего и кратчайшего покрывающего деревьев в графе.

3. Что в теории графов подразумевается под терминами “корень”, “ветвь”, “лес”?

4. Каким образом определяется число покрывающих деревьев в произвольном полном графе?

5. Сформулируйте задачу о лабиринте.

6. Приведите теорему для определения дерева.

7. Запишите теорему Кэли и следствие из нее.

8. Приведите теорему о каркасе минимального веса в графе.

9. В чем заключаются алгоритмы Краскала и Прима?

10. Приведите леммы о деревьях Штейнера.

Дата добавления: 2015-10-26