
Читайте также:
|
Пример 1. Определить цикломатическое число графа G = (X, U), изображенного на рис. 17.3.

Рис. 17.3. Граф G
Решение: из рис. 17.3видно, что исходный граф состоит из двух компонент связности, причем ½X½ = 8; ½U½ = 11, т.е. граф G имеет 8 вершин и 11 ребер. Подставив эти числа в формулу (3.1), получим g(G) = 11 - 8 + 2 = 5. Следовательно, из исходного графа G необходимо удалить пять ребер для того, чтобы получилось дерево. Теперь необходимо определить, какие именно ребра мы должны удалить.
Как уже было сказано выше, на каждом шаге удаляется ребро, образующее хотя бы один цикл. В заданном графе присутствуют две компоненты связности. Проанализировав каждое ребро первой компоненты, мы приходим к выводу, что в данном случае удаление любого ребра приведет к разрыву одного из имеющихся циклов поэтому можно удалить любое ребро. Пусть это будет ребро (x 1 – x 2). Удалим шаг за шагом, например, ребра (x 2 – x 3); (x 3 – x 4). Как видно, в первой компоненте не осталось больше ни одного цикла. Теперь рассмотрим вторую компоненту. Здесь мы можем удалить, к примеру, ребра (x 5 – x 6); (x 6 – x 7). Мы удалили из исходного графа пять ребер. В результате получили лес, состоящий из двух деревьев, изображенных на рис. 17.4.
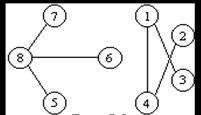
Рис. 17.4. Лес, состоящий из двух п окрывающих деревьев на основе графа G
Пример 2. Определить хроматическое число и раскраску графа, изображенного на рис. 17.5.

Рис. 17.5. Граф G
Решение: для решения поставленной задачи воспользуемся последовательным алгоритмом раскраски графа.
1. Подсчитываем локальные степени вершин графа G и составляем список вершин в порядке не возрастания их локальных степеней:
 .
.
2. Выбираем из списка вершину x 4: P1 = { x 4}.
3. Просматриваем список на предмет нахождения несмежных вершин. Выбираем ближайшую несмежную вершину. Это вершина x 7: P1 = { x 4, x 7}.
4. Продолжаем процесс просмотра. Выбираем вершину x 2 - несмежную вершинам x 4 и x 7, включенным в подмножество P1. Теперь P1 = { x 4, x 7, x 2}.
5. Просматриваем список дальше, и так как в списке больше нет вершин, несмежных вершинам подмножества P1, окрашиваем вершины этого подмножества в первый цвет и удаляем их из списка. После удаления список примет вид
 .
.
6. Выбираем вершину x 8: P2 = { x 8}.
7. Выбираем вершину x 1: P2 = { x 8, x 1}.
8. Выбираем вершину x 3: P2 = { x 8, x 1, x 3}.
9. Выбираем вершину x 6: P2 = { x 8, x 1, x 3, x 6}.
10. В списке нет больше вершин, несмежных вершинам подмножества P2. Окрашиваем вершины этого подмножества во второй цвет и удаляем их из списка.
11. В списке остается только одна вершина – x 5. Эта вершина окрашивается в третий цвет.
Таким образом, для раскраски графа нам потребовались три краски, следовательно, хроматическое число: c(G) = 3.
Пример 3. Привести пример полного двудольного графа G = (X1, X2, U), при условии, что ½X1½ = 3; а ½X2½ = 4.
Ответ: пример полного двудольного графа соответствующего исходным условиям показан на рис. 17.6.
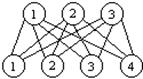
Рис. 17.6. Полный двудольный граф
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что такое цикломатическое число графа? Что показывает цикломатическое число графа?
2. Каким образом определяется цикломатическое число графа?
3. Что такое коцикломатическое число графа?
4. Дайте определение фундаментального цикла?
5. Каким образом можно построить матрицу фундаментальных циклов?
6. Что такое хроматическое число графа?
7. Какие оценки хроматического числа вы знаете? Какие методы нахождения хроматического числа обычно используются при решении практических задач?
8. Что такое раскраска вершин графа? Каким образом производится раскраска вершин графа?
9. Какой граф называется двудольным?
10. Дайте определение полного двудольного графа.
Дата добавления: 2015-10-26; просмотров: 174 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Цикломатическое и хроматическое числа графа | | | Числа внутренней и внешней устойчивости графа |