Задания для самостоятельной работы

1. Для произвольного G = (X, U) графа определить число внутренней устойчивости.

2. Определить число внутренней устойчивости произвольного графа G = (X, U) и построить семейство независимых подмножеств.

3. Для произвольного графа G = (X, U) построить раскраску на основе алгоритма выделения независимых подмножеств.

4. Для произвольного графа G = (X, U) определить число внешней устойчивости и применить алгоритм выделения минимальных внешне устойчивых подмножеств.

5. Постройте структурную схему алгоритма нахождения семейства независимых подмножеств.

6. Запишите псевдокод алгоритма построения семейства независимых подмножеств.

7. Постройте структурную схему алгоритма определения семейства доминирующих подмножеств в графе.

8. Постройте псевдокод алгоритма определения семейства доминирующих подмножеств в графе.

9. Запишите псевдокод алгоритма раскраски графа путем нахождения минимального покрытия независимыми подмножествами.

10. Постройте структурную схему алгоритма раскраски графа путем нахождения минимального покрытия независимыми подмножествами.

Числа внутренней и внешней устойчивости относятся к инвариантам графа. Они позволяют определить специальные группы вершин в графах.

Планарность графов

Методы теории графов позволяют решать многие технические и теоретические задачи, такие как расчет электронных схем, задачи сетевого планирования, микроэлектроники, искусственного интеллекта и др. Это объясняется тем, что граф, сохраняя всю наглядность и содержательность объекта, позволяет строить формальные модели живой и неживой природы, которые легко обрабатываются на ЭВМ. Данный раздел посвящен обзору важнейшего раздела теории графов – планарности. Проблемы планарности графов связаны с возможностью плоского (без пересечений ребер) изображения графа, минимизации пересечений ребер, разбиения непланарного графа на плоские и планарные подграфы и суграфы.

Плоские и планарные графы

Изучение планарных графов начал Эйлер в его исследованиях полиэдров. С каждым полиэдром связан граф, состоящий из точек и линий полиэдра. Говорят, что граф укладывается на поверхность S, если его можно нарисовать на S так, что никакие два его ребра не пересекаются. Граф называется планарным, если его можно уложить на плоскости без пересечений. Плоский граф, это граф уже расположенный на плоскости без пересечений.

Области, определяемые плоским графом (ПЛГ), называются его внутренними гранями или просто гранями. Если границей грани ПЛГ является простой цикл, то иногда под гранью понимают этот цикл. ПЛГ (рис. 17.9) имеет две внутренние грани f1, f2 и одну внешнюю – f3. Неограниченная область называется внешней гранью.

Рис. 17.9. Плоский граф с тремя гранями

Плоской картой называется связный ПЛГ вместе со всеми его гранями. Уравнение (теорема) Эйлера для плоской карты с n–вершинами, m–ребрами и f–гранями запишется как

Теорема 17.4

n – m + f = 2. (17.13)

Следствие 17.1. Если G – плоская (n, m) – карта, в которой каждая грань является С -циклом (т.е. циклом длиной С, состоящим из С ребер), то

(17.14)

и

m = С f / 2. (17.15)

Максимальным планарным графом (МПГ) называется граф, который при добавлении любого ребра перестает быть планарным.

Следствие 17.2. Если G – МПГ, то каждая его грань является треугольником и

m = 3n – 6. (17.16)

Если G – плоский граф, у которого любая грань есть 4–цикл, то

m = 2n – 4. (17.17)

Так как наибольшим числом ребер в ПЛГ обладает граф, у которого каждая грань есть треугольник, то получаем необходимое условие планарности графа в терминах числа ребер.

Следствие 17.3. Графы K₅ и K_3,3 не являются планарными.

На рис. 17.10,а показан граф K₅, а на рис. 17.10,б – K_3,3.

а

б

Рис. 17.10. Полный граф K₅ (а), полный двудольный граф K_3,3 (б)

Доказательство. K₅ есть граф c 5 вершинами 10 ребрами, и он не может быть планарным, так как m= 10 > 3n - 6 = 9. Для K_3,3 имеем m = 9 > 2n – 4 = 8, что и доказывает следствие 17.3.

Легко видеть, что каждый подграф ПЛГ – планарен, а любой граф, содержащий в качестве подграфа непланарный граф (НПГ), сам не может быть планарным. Отсюда вытекает, что K₅ и K_3,3 – по существу единственные непланарные графы в том смысле, что любой НПГ содержит один из них.

Два графа гомеоморфны (или тождественны с точностью до вершины степени 2), если они могут быть получены из одного и того же графа включением (добавлением) в его ребра новых вершин степени 2.

Л.С. Понтрягин в 1927г. доказал, но не опубликовал критерий планарности.

К. Куратовский в 1930 г. независимо от Л.С. Понтрягина получил тот же результат.

Теорема 17.5. (Понтрягин – Куратовский). Граф планарен тогда и только тогда, когда он не содержит подграфа гомеоморфного графам K₅ или K_3,3.

Граф G называется стягиваемым к графу Н, если Н можно получить из G с помощью некоторой последовательности элементарных стягиваний. Например, на рис. 3.11 показано как граф Петерсона стягивается в K₅. Здесь произошло стягивание в новую вершину w_i любого из пяти ребер (u_i, v_i), соединяющего пятиугольник с пентаграммой (звездой). Т.е. K₅ получается из графа Петерсона стягиванием 5 ребер внутреннего цикла с внешним (рис. 17.12).

Теорема 17.6. (Харари – Татт). Граф планарен тогда и только тогда, когда он не содержит подграфов, стягиваемых в K₅ или K_3,3.

Рис. 17.11. Граф Петерсона

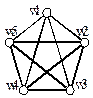
Рис. 17.12. Граф K₅, полученный из графа Петерсона

Уитни связал планарность графов с существованием двойственных графов (ДГ). Для данного плоского графа G его геометрический ДГ, т.е. ГДГ G* строится так:

· поместим в каждую область G, включая внешнюю, по одной вершине G*;

· если две области имеют общее ребро u, соединим помещенные в них вершины ребром u*, пересекающим только u.

Данный процесс показан, например, для графа G (рис. 17.13).

Рис. 17.13. Пример построения ГДГ

Здесь ребра ГДГ G* штриховые линии. G* – имеет петлю, тогда когда в G есть концевая вершина в примере с рис. 3.10,в. G* – имеет кратные ребра, когда две области G содержат, по крайней мере, два общих ребра.

Таким образом, двусвязный плоский граф имеет всегда в качестве двойственного или граф, или мультиграф. ГДГ плоского графа G также плоский, а ГДГ к ГДГ – это первоначальный граф G.

Толщина графа – наименьшее число планарных графов, объединение которых есть G. Крупность (шероховатость, зернистость) графа – наибольшее число непланарных подграфов в G не пересекающихся по ребрам (т.е. подграфов не имеющих общих ребер). Число скрещиваний (пересечений) графа – наименьшее число пересечений ребер, которое должно быть при расположении G на плоскости.

Эвристики для определения планарности

Все существующие методы определения планарности разбивают на два класса. В первый класс входит методы, основанные на проверке критериев:

а) Понтрягина – Куратовского.

б) Харари – Татта.

в) Уитни.

г) Существования абстрактно – двойственного графа.

д) Мак – Лейна.

Во второй класс входят эвристические методы в той или иной степени использующие критерии первого класса это:

a) Алгоритм Бадера.

b) Циклические методы.

c) Матричные методы.

d) Комбинированные методы.

Так как неорграф планарен тогда и только тогда, когда все его связные компоненты планарны, то достаточно рассматривать лишь связные неорграфы. Очевидно, что неорграф планарен тогда и только тогда, когда все его двусвязные компоненты планарны. Поэтому, если неорграф (далее граф) является разделимым, можно разложить его на двусвязные компоненты и рассматривать их отдельно. Поскольку кратные ребра и петли всегда можно добавить к графу или удалить из него без нарушения свойств планарности, достаточно рассматривать только простые графы.

Итак, для определения планарности будем предполагать, что исходный граф неориентированный, простой и двухсвязный. Согласно теореме Понтрягина – Куратовского неплоский граф имеет, по крайней мере, 9 ребер.

Сущность алгоритма заключается в следующем. Записывается матрица смежности, анализируя которую определяются пресечения ребер графа. Затем строится граф (матрица) пересечений. Далее определяется двудольность (бихроматичность) графа пересечения.

Теорема 17.7 (Бадер). Если граф пересечений двудольный, то исходный граф планарный.

Доказательство следует из того, что в двудольном графе можно выделить два подмножества несмежных вершин У’, У’’, таких, что У’ È У’’ = У и У’ Ç У’’ = Æ. Граф пересечений G’ = (У, V) для графа G = (X, U) определяется так, что У «U’, где U’ - подмножество пересекающихся ребер.

Алгоритм рассмотрим на примере. Пусть дан G = (У, V), имеющий известный гамильтонов цикл (ГЦ). Расположим его на плоскости (рис 17.14). По известной методике определим пересечения ребер внутри ГЦ. Далее строится граф пересечений G’ = (У,V) (рис. 17.15). Теперь необходимо воспользоваться теоремой Бадера и определить является ли граф G’ двудольным или нет.

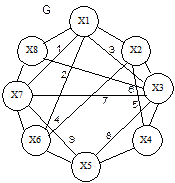
Рис. 17.14. Граф G

Рис. 17.15. Граф пересечений G`

Согласно теореме Кэнига граф двудолен, если в нем нет циклов нечетной длины. Поэтому для определения двудольности графа G’ можно предложить несколько основных эвристик:

Э1. Определить все циклы графа пересечений G’, если среди них нет нечетных, то исходный граф G планарен.

Э2. Проверить, является ли граф пересечений G’ деревом. Если да, то G’ – двудольный, так как всякое дерево двудольный граф. Следовательно, если G’ – дерево, то G – планарный граф.

Э3. Определить систему МВУП (независимых подмножеств) графа G’. Если среди семейства МВУП найдутся, такие два подмножества П₁, П₂, что

П₁ È П₂ = У, П₁ Ç П₂ = Æ,

то граф G’ - двудольный, а G - планарный.

Например, для графа G’ (рис. 17.15)

П₁ = {y₁, y₂, y₄, y₅}, П₂ = {y₆, y₇, у₃, y₈, y₉}, G’ = (У, V), П₁ È П₂ = У, П₁ Ç П₂ = Æ.

Граф G’, представленный в виде двудольного, показан на рис. 3.16. Очевидно, что граф G – планарный (рис. 3.14). Так ребра G, соответствующие П₁, можно расположить без пересечений внутри ГЦ, а ребра, соответствующие П₂ – внутри ГЦ, или наоборот. Плоское изображение графа (рис. 17.14) показано на рис. 17.17).

Рис. 17.16. Двудольный граф G

Рис. 17.17. Плоское преображение графа G

Основная стратегия определения планарности состоит в том, чтобы в графе G найти цикл С, разместить С на плоскости в виде простой замкнутой кривой, разложить оставшуюся часть G – C на непересекающиеся по ребрам пути и затем попытаться разместить внутри С либо целиком вне С. Если это удалось для всего графа G, то он планарен, в противном случае он не планарен. Трудность реализации алгоритма заключается в том, что при размещении пути можно выбрать либо внутренность, либо внешность С и необходимо обеспечить, чтобы неправильный выбор области размещения на ранней стадии не устранял возможности размещения последующих путей. Это может привести к неверному заключению, что планарный граф непланарен.

Дата добавления: 2015-10-26