
|
Читайте также: |
планетарного редуктора
Визначення передаточного відношення зубчастого механізму привода.
Загальне передаточне відношення зубчастого механізму привода:

де  – частота обертання вала електродвигуна привода,
– частота обертання вала електродвигуна привода, 
 – частота обертання кривошипа шарнірно-важільного механізму,
– частота обертання кривошипа шарнірно-важільного механізму, 
Оскільки передаточний механізм двоступінчастий, перший ступінь у ньому – планетарний механізм, а другий – простий зубчастий, то

де  – передаточне відношення планетарного редуктора від колеса 1 до водила
– передаточне відношення планетарного редуктора від колеса 1 до водила 
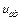 – передаточне відношення простої зубчастої передачі від колеса
– передаточне відношення простої зубчастої передачі від колеса  до колеса
до колеса 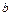 .
.
Передаточне відношення простої зубчастої передачі:

Тоді передаточне відношення планетарного редуктора:

Вибір чисел зубців зубчастих коліс планетарного редуктора.
Вибір чисел зубців зубчастих коліс планетарного редуктора здійснюємо за такими умовами:
– забезпечення заданого передаточного відношення;
– співвісність;
– сусідство;
– складання;
– правильність зачеплення.
З умови співвісності  та формули для передаточного відношення планетарного редуктора
та формули для передаточного відношення планетарного редуктора  визначаємо відношення
визначаємо відношення 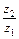 :
:

Підберемо такі числа зубців коліс планетарного редуктора, щоб  . При цьому для збільшення можливості задоволення умови складання
. При цьому для збільшення можливості задоволення умови складання  і
і  повинні бути кратними числу сателітів
повинні бути кратними числу сателітів  . Найбільш вигідне число сателітів
. Найбільш вигідне число сателітів  Оскільки
Оскільки  , то приймаємо число зубців малого центрального колеса
, то приймаємо число зубців малого центрального колеса 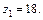 Тоді число зубців сателіта:
Тоді число зубців сателіта:

Одержане значення  заокруглюємо до числа, що кратне числу сателітів
заокруглюємо до числа, що кратне числу сателітів  . Приймаємо
. Приймаємо 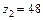 .
.
Число зубців  великого центрального колеса дорівнює:
великого центрального колеса дорівнює:

Фактичне передаточне відношення планетарного редуктора:

Відхилення фактичного передаточного відношення планетарного редуктора  від заданого
від заданого  знаходиться в допустимих межах, оскільки:
знаходиться в допустимих межах, оскільки:

Перевіряємо умову складання:

Умова виконується, оскільки одержане число – ціле.
Перевіряємо умову сусідства за формулою:
 (5.4)
(5.4)
Отже, умова (5.4) виконується. Таким чином, остаточно приймаємо значення чисел зубців планетарного редуктора:
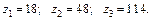
Визначаємо початкові діаметри зубчастих коліс планетарного редуктора (усі колеса нульові):
малого центрального колеса 1

сателітів 2

великого центрального колеса 3

У масштабі  викреслюємо схему планетарного редуктора в двох проекціях: у площині, яка містить центральну вісь редуктора, і в площині, перпендикулярній до неї (див. аркуш 3 (додаток В)). На кресленні, що розташоване у площині обертання зубчастих коліс, позначаємо характерні точки:
викреслюємо схему планетарного редуктора в двох проекціях: у площині, яка містить центральну вісь редуктора, і в площині, перпендикулярній до неї (див. аркуш 3 (додаток В)). На кресленні, що розташоване у площині обертання зубчастих коліс, позначаємо характерні точки:  і
і  – центри обертання коліс відповідно
– центри обертання коліс відповідно
1 і 2;  – полюс зачеплення пари коліс 1 і 2;
– полюс зачеплення пари коліс 1 і 2;  – точка, яка лежить на водилі
– точка, яка лежить на водилі  і збігається з точкою
і збігається з точкою  ;
;  – миттєвий центр обертання сателіта 2.
– миттєвий центр обертання сателіта 2.
Визначаємо швидкість точки  , яка лежить на колесі 1:
, яка лежить на колесі 1:

де  – кутова швидкість колеса 1,
– кутова швидкість колеса 1, 
Відкладаємо вектор цієї швидкості у вигляді відрізка 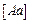 і з’єднуємо кінець цього вектора з центром
і з’єднуємо кінець цього вектора з центром  . Пряма
. Пряма 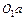 зображає закон розподілення лінійних швидкостей точок центрального колеса 1. Масштаб картини лінійних швидкостей:
зображає закон розподілення лінійних швидкостей точок центрального колеса 1. Масштаб картини лінійних швидкостей:

Точка  є миттєвим центром обертання сателіта 2, тому пряма
є миттєвим центром обертання сателіта 2, тому пряма 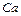 , яка з’єднує точку
, яка з’єднує точку  з точкою
з точкою  , зображає закон розподілення лінійних швидкостей точок сателіта. Цей закон використаємо для визначення швидкості центра сателіта
, зображає закон розподілення лінійних швидкостей точок сателіта. Цей закон використаємо для визначення швидкості центра сателіта  провівши через точку
провівши через точку  горизонталь до її перетину в точці
горизонталь до її перетину в точці 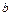 з прямою
з прямою 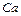 . Оскільки точка
. Оскільки точка  належить також і водилу
належить також і водилу  центром якого є точка
центром якого є точка  , то пряма
, то пряма  зображатиме закон розподілення лінійних швидкостей точок водила. Швидкість точки
зображатиме закон розподілення лінійних швидкостей точок водила. Швидкість точки  яка лежить на водилі, буде зображатися відрізком
яка лежить на водилі, буде зображатися відрізком 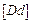 . Отже, передаточне відношення планетарного редуктора виражається через відношення відповідних відрізків картини лінійних швидкостей:
. Отже, передаточне відношення планетарного редуктора виражається через відношення відповідних відрізків картини лінійних швидкостей:
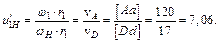
Відносна похибка

знаходиться в допустимих межах, де  – фактичне передаточне відношення планетарного редуктора, яке визначене аналітично.
– фактичне передаточне відношення планетарного редуктора, яке визначене аналітично.
Для визначення передаточного відношення планетарного редуктора зручно використовувати картину кутових швидкостей, яку будуємо так: на вертикальній прямій  відкладаємо відрізок
відкладаємо відрізок 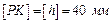 і проводимо через точку
і проводимо через точку  горизонтальну лінію
горизонтальну лінію  а через точку
а через точку  проводимо промені
проводимо промені 

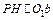 до перетину з лінією
до перетину з лінією  . Одержані точки на лінії
. Одержані точки на лінії  позначимо відповідно 1, 2,
позначимо відповідно 1, 2, 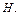 Відрізки
Відрізки 

 зображають у деякому масштабі кутові швидкості відповідно ланок 1, 2,
зображають у деякому масштабі кутові швидкості відповідно ланок 1, 2, 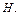 Отже, передаточне відношення планетарного редуктора виражається через відношення відповідних відрізків картини кутових швидкостей:
Отже, передаточне відношення планетарного редуктора виражається через відношення відповідних відрізків картини кутових швидкостей:

Масштаб картини кутових швидкостей:

Відносна похибка

знаходиться в допустимих межах.
Дата добавления: 2015-10-24; просмотров: 92 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Побудова картини евольвентного зубчастого зачеплення | | | Единый сердечный диполь |