Профілювання кулачка

Для побудови теоретичного профілю кулачка використаємо метод оберненого руху механізму. Побудову проводимо в масштабі Якщо умовно надати кулачковому механізму додаткового обертового руху навколо центра обертання кулачка з кутовою швидкістю , то кулачок буде нерухомим, а штовхач разом із напрямною буде обертатися навколо кулачка, при цьому вістря штовхача переміщатиметься на теоретичному профілі кулачка і, крім цього, відносно напрямної так, як і в дійсному русі.

Будуємо профіль кулачка за таким порядком.

1. З довільно вибраної точки А, яка прийнята за центр обертання кулачка, будуємо основне коло кулачка радіусом:

2. Відкладаємо ексцентриситет , який визначає положення осі руху штовхача відносно центра обертання кулачка, і проводимо радіусом коло. У нашому випадку .

3. З точки перетину основного кола та осі руху штовхача відкладаємо його максимальний хід у масштабі , тобто:

одержимо точку . Радіус визначає максимальний радіус кулачка .

4. Від лінії проти обертання кулачка відкладаємо фазові кути .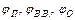

5. Будуємо положення осі штовхача в оберненому русі. Для цього ділимо фазові кути і на 10 рівних частин (у відповідності до діаграм руху штовхача) для кожного періоду і проводимо промені і т. д.). Ці промені визначають положення осі штовхача в оберненому русі.

6. Маючи діаграму переміщень штовхача , знаходимо положення вістря штовхача у дійсному русі (точки і т. д. на осі штовхача). Наприклад, щоб знайти точку на осі штовхача необхідно виміряти вертикальний відрізок у на діаграмі , а потім знайти відрізок , який потрібно відкласти від точки на осі штовхача. Інші точки і т. д. на осі штовхача знаходяться аналогічно.

7. Будуємо теоретичний профіль кулачка. Для цього з центра кулачка радіусами і т. д. робимо дугові засічки на відповідних положеннях штовхача і т. д. в оберненому русі. Одержані точки ( і т. д.) з’єднуємо плавною кривою, яка буде теоретичним профілем кулачка.

На ділянках верхнього і нижнього стояння профіль кулачка буде окреслений дугами кола відповідних радіусів.

8. Вибираємо радіус ролика з умови контактної міцності матеріалів кулачка і ролика. Рекомендується приймати [3]:

Приймаємо , який на кресленні зображений відрізком:

(4.2)

Вибраний радіус ролика перевіряємо з умови усунення самоперетину практичного профілю кулачка. При цьому необхідно, щоб виконувалась умова:

, (4.3)

де – мінімальний радіус кривизни теоретичного профілю кулачка. Мінімальний радіус кривизни визначається наближено як радіус кола, що проходить через три точки, які вибираються на ділянці теоретичного профілю кулачка, де можна очікувати мінімальне значення радіуса кривизни. У нашому випадку

Отже, умова (4.3) виконується.

5. СИНТЕЗ І АНАЛІЗ ЗУБЧАСТИХ ПЕРЕДАЧ

5.1. Вибір коефіцієнтів зміщення циліндричних

евольвентних зубчастих коліс зовнішнього зачеплення

Знайдемо коефіцієнти зміщення для пари зубчастих коліс і простої передачі механізму привода, виходячи з умов відсутності підрізання зубців та забезпечення максимального торцевого коефіцієнта перекриття. Надалі надамо шестерні індекс 1, а колесу індекс 2. Використовуючи блокувальний контур для і з [3], с. 297, знаходимо:

5.2. Розрахунок геометричних параметрів

циліндричної евольвентної передачі зовнішнього зачеплення

У всіх варіантах курсового проекту вважається, що зубчасті колеса нарізаються інструментальною рейкою зі стандартними параметрами за ГОСТ 13755:

– кут профілю вихідного контуру

– коефіцієнт висоти головки зубця

– коефіцієнт радіального зазору

– коефіцієнт радіуса кривини перехідної кривої

5.2.1. Коловий крок по дузі ділильного кола

5.2.2. Кут зачеплення

де – коефіцієнт суми зміщень;

– сумарне число зубців коліс простої передачі.

Кут зачеплення знаходимо за таблицею значень евольвентної функції ([10], с. 14 – 15).

5.2.3. Міжосьова відстань

5.2.4. Ділильні діаметри

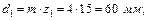
5.2.5. Початкові діаметри

де 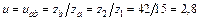– передаточне відношення простої передачі механізму привода.

5.2.6. Коефіцієнт сприймального зміщення

5.2.7. Коефіцієнт зрівнювального зміщення

5.2.8. Діаметри вершин

5.2.9. Діаметри западин

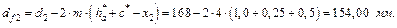
5.2.10. Діаметри основних кіл

5.2.11. Товщина зубців по дузі ділильного кола

5.2.12. Ширина западин по дузі ділильного кола

5.2.13. Висота зубців

5.2.14. Кутовий крок зубців

5.2.15. Товщина зубців по дузі кола вершин

де – кут профілю зубця шестерні в точці на колі вершин;

– кут профілю зубця колеса в точці на колі вершин.

5.2.16. Коефіцієнт торцевого перекриття

Перевіряємо умови існування зубчастої передачі:

(5.1)

Оскільки усі умови (5.1) виконуються, то розрахунок геометричних параметрів циліндричної евольвентної передачі зовнішнього зачеплення завершено.

Дата добавления: 2015-10-24