Для дванадцяти положень механізму

Побудову планів швидкостей розглянемо на прикладі шостого положення механізму. З полюса (див. аркуш 1 (додаток А) або рис. 2.1) плану швидкостей за напрямом обертання кривошипа перпендикулярно відкладаємо в масштабі вектор швидкості точки А, величина якого:

,

Рис. 2.1. План швидкостей для шостого положення механізму

де –кутова швидкість кривошипа, .

Приймаємо довжину відрізка, який зображає вектор швидкості точки А, 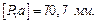Тоді масштаб плану швидкостей:

.

Швидкість точки B ₂, яка лежить на кулісі АС і в даний момент збігається з точкою В, що належить каменю 3 чи стояку 0, визначаємо з рівнянь:

(2.1)

З точки а проводимо напрям вектора відносної швидкості (перпендикулярно до АВ), а через те, що , то з полюса проводимо напрям вектора швидкості 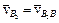(паралельно АВ). Точка перетину цих ліній і є шукана точка , а відрізки і відповідно у масштабі зображають вектори швидкостей і , тобто:

;

.

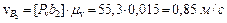Для визначення швидкості точки С ₂, яка належить кулісі 2 і в даний момент збігається з точкою С, що належить ланкам 4 і 5, використаємо теорему подібності плану швидкостей ланці, на підставі якої можна скласти пропорцію:

.

Тоді

.

Відклавши від точки а на продовженні відрізка відрізок 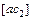, знаходимо положення точки 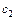, поєднавши яку з полюсом , отримаємо в масштабі швидкість точки С ₂:

.

Швидкість точки С, яка належить повзунам 4 і 5, можна виразити через швидкості точок С ₂ і С ₀. Вектор швидкості точки С ₂ відомий за величиною і за напрямом; швидкість точки С ₀, що належить стояку і також збігається з точкою С, . Тоді можна записати векторні рівняння:

(2.2)

На плані швидкостей з точки 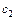проводимо паралельно кулісі АС пряму, яка визначає напрям швидкості 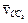, а з полюса проводимо лінію паралельну напрямній, що визначає напрям швидкості точки С відносно стояка. Відрізки і у масштабі зображають вектори швидкостей:

;

.

Для визначення швидкості центра мас S₂ куліси використаємо теорему подібності плану швидкостей ланці, склавши пропорцію:

, (2.3)

з якої знаходимо

.

З’єднавши точку з полюсом плану швидкостей, отримаємо відрізок , який у масштабі визначає значення швидкості:

.

Значення кутової швидкості куліси знаходимо за формулою:

.

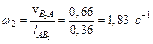Щоб визначити напрям кутової швидкості 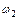, розглянемо обертання ланки 2 відносно точки А. Напрям руху точки В₂ відносно точки А визначається вектором швидкості . Подумки переносимо цей вектор у точку В механізму і вважаємо точку А нерухомою. Отже, ланка АС відносно точки А обертається за годинниковою стрілкою.

Плани швидкостей для інших положень механізму будуємо аналогічно (див. аркуш 1 (додаток А)). Отримані значення відрізків, які зображають вектори швидкостей, і значення швидкостей наведені у табл. 2.1.

Таблиця 2.1

Дата добавления: 2015-10-24