Механізму та зрівноважувальної сили

Силовий аналіз групи 4–5.

Визначення реакцій у кінематичних парах починаємо з аналізу
групи 4–5.

Прикладаємо до ланок 4 і 5 усі зовнішні сили, включаючи сили інерції, дію ланок 0 і 2 замінюємо реакціями і .

Реакцію прикладаємо в довільній точці. Напрям її визначається з умови рівноваги повзуна 4:

,

де – реакція ланки 5 на повзун 4.

Оскільки ланка АС і повзун 4 утворюють поступальну пару, то реакція напрямлена перпендикулярно до осі куліси АС, якщо не враховувати сили тертя. Отже, вектор також буде напрямлений перпендикулярно до осі куліси АС і .

Складаємо рівняння рівноваги групи 4-5 під дією всіх прикладених сил:

. (3.1)

У цьому рівнянні два вектори і відомі тільки за напрямом (вони підкреслені однією рискою), а інші вектори відомі повністю
(вони підкреслені двома рисками). Отже, рівняння розв’язується методом плану сил.

На підставі рівняння (3.1) будуємо план сил у масштабі . Використовуючи побудований план сил, знаходимо невідомі реакції:

;

,

де – відрізки у міліметрах, які зображають відповідні реакції на плані сил.

Визначаємо точку прикладання реакції , для чого складаємо рівняння моментів усіх сил, які діють на групу 4–5, відносно
точки С:

,

звідки отримуємо . Отже, реакція прикладена в точці С і напрямлена вгору.

Силовий аналіз групи 2–3.

На ланки цієї групи, крім сил тяжіння і , сили інерції і моменту сил інерції , діють ще реакції і . Реакція прикладена в точці С і за величиною дорівнює , але протилежно їй напрямлена. Реакції і проходять відповідно через центри шарнірів А і В, а їх напрями і величини невідомі.

Для визначення реакції складаємо векторне рівняння сил, що діють на ланку 2. Для цього подумки відкидаємо ланку 3 і замінюємо її дію реакцією , яка напрямлена перпендикулярно до лінії відносного руху ланок 2 і 3, тобто перпендикулярно до лінії АС:

. (3.2)

Рівняння (3.2) розв’язується графічно після визначення величини реакції з рівняння моментів сил, що діють на ланку 2 відносно
точки А:

,

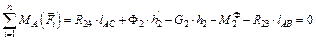де

Тоді

На підставі рівняння (3.2) будуємо план сил у масштабі і визначаємо реакцію:

.

Для визначення реакції складаємо векторне рівняння рівноваги сил, що діють на ланку 3. На цю ланку діють сили 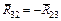, і .
Тоді

(3.3)

Розв’язуючи графічно на об’єднаному плані сил групи 2–3 рівняння (3.3), одержимо:

Силовий аналіз механізму І класу.

На кривошип 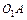діють такі сили: реакція , реакція , сила тяжіння . Для рівноваги ланки 1, крім цих сил, необхідно врахувати ще зрівноважувальну силу 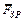, яку прикладаємо в точці А перпендикулярно до кривошипа 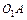[1, 2, 13]. Зрівноважувальна сила для даного механізму є рушійною силою, прикладеною збоку привода.

Зрівноважувальну силу визначаємо з умови рівноваги кривошипа 1 відносно точки :

,

де

Тоді

.

Для визначення реакції будуємо план сил у масштабі на підставі векторного рівняння:

звідки маємо

3.3. Визначення зрівноважувальної сили

методом М.Є. Жуковського

Для визначення методом М.Є. Жуковського будуємо повернутий на 90° проти обертання кривошипа план швидкостей, на якому прикладаємо у відповідних точках усі зовнішні сили, що діють на ланки механізму, включаючи сили інерції та зрівноважувальну силу. Момент сил інерції замінюємо парою сил , які за величиною дорівнюють:

З рівняння рівноваги повернутого плану швидкостей під
дією прикладених сил відносно полюса визначаємо зрівноважувальну
силу:

Порівнюємо величину зрівноважувальної сили, що отримана методом планів і методом важеля М.Є. Жуковського :

Розбіжність значень знаходиться в допустимих межах.

Дата добавления: 2015-10-24