
Читайте также:
|
Наиболее точный способ определения тесноты и характера корреляционной связи – нахождение коэффициента корреляции. Коэффициент корреляции есть число, определяемое по формуле:
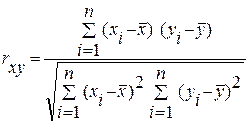 (5.2.1)
(5.2.1)
где rху – коэффициент корреляции; xi – значения первого признака; уi – значения второго признака;  – средняя арифметическая значений первого признака,
– средняя арифметическая значений первого признака, 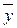 – средняя арифметическая значений второго признака
– средняя арифметическая значений второго признака
Число коэффициента корреляции дает возможность установить наличие, тесноту и характер связи.
1. Если коэффициент корреляции равен нулю, связь между признаками отсутствует.
2. Если коэффициент корреляции равен единице, связь между признаками столь велика, что превращается в функциональную.
3. Абсолютная величина коэффициента корреляции не выходит за пределы интервала от нуля до единицы:
0 < | rxy | < 1.
Это дает возможность ориентироваться на тесноту связи: чем величина коэффициента ближе к нулю, тем связь слабее, а чем ближе к единице, тем связь теснее.
4. Знак коэффициента корреляции «плюс» означает прямую корреляцию, знак «минус» – обратную.
Для пользования формулой (5.2.1) построим таблицу, которая обеспечит необходимую последовательность в подготовке чисел для нахождения числителя и знаменателя коэффициента корреляции.
Так для примера 5.1.1 нахождение коэффициента корреляции в соответствии с формулой (5.2.1) можно представить следующим образом (табл. 5.2.1).
Таблица5.2.1.
| хі | уі | (хі- 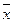 ) )
| (уі- 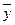 ) )
| (хі- 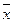 )(уі- )(уі- 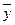 ) )
| (хі- 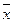 )2 )2
| (уі- 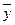 )2 )2
|
| 14,00 | 12,10 | —1,70 | —2,30 | +3,91 | 2,89 | 5,29 |
| 14,20 | 13,80 | —1,50 | —0,60 | +0,90 | 2,25 | 0,36 |
| 14,90 | 14,20 | —0,80 | —0,20 | +0,16 | 0,64 | 0,04 |
| 15,40 | 13,00 | —0,30 | —1,40 | +0,42 | 0,09 | 1,96 |
| 16,00 | 14,60 | +0,30 | +0,20 | +0,06 | 0,09 | 0,04 |
| 17,20 | 15,90 | +1,50 | +1,50 | +2,25 | 2,25 | 2,25 |
| 18,10 | 17,40 | +2,40 | +2,00 | +4,80 | 5,76 | 4,00 |
| 109,80 | 101,00 | 12,50 | 13,97 | 13,94 |

Таким образом, вычисленный в примере 5.1.1 коэффициент корреляции rxy =+0,9. позволяет сделать такие выводы: существует корреляционная связь между величиной мышечной силы правой и левой кистей у исследуемых школьников (коэффициент rxy =+0,9 отличен от нуля), связь очень тесная (коэффициент rxy =+0,9 близок к единице), корреляция прямая (коэффициент rxy = +0,9 положителен), т. е. с увеличением мышечной силы одной из кистей увеличивается сила другой кисти.
При вычислении коэффициента корреляции и пользовании его свойствами следует учесть, что выводы дают корректные результаты в том случае, когда признаки распределены нормально и когда рассматривается взаимосвязь между большим количеством значений обоих признаков.
5.3. Корреляционные отношения
Отражением нелинейной (криволинейной) корреляции являются корреляционные отношения. Корреляционное отношение hу/х указывает на зависимость признака у от признака х; отношение h/хy – зависимость признака х от у. Эти величины определяются по формулам:
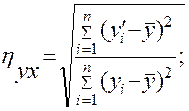 (5.3.1)
(5.3.1)
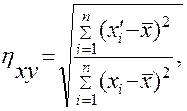 (5.3.2)
(5.3.2)
где hу/х; hx/y – корреляционные отношения; xi, yi – варианты признака х и признака у;  – средние арифметические обоих признаков; хi', уi' – частные средние признаков х и у.
– средние арифметические обоих признаков; хi', уi' – частные средние признаков х и у.
Для определения частных средних хi', уi' находят средние арифметические второго признака среди соответствующих им одинаковых вариантов первого признака. Использование корреляционными отношениями основано на свойстве этих величин, а именно: корреляционное отношение, всегда положительное, не выходит за пределы от нуля до единицы:
Следовательно, как и в случае с коэффициентом корреляции, чем выше корреляционное отношение, тем теснее связь между исследуемыми признаками, чем ниже— тем слабее.
Поскольку пара коррелируемых признаков отражается двумя отношениями, представляется возможность выявить ведущий признак.
Допустим, в результате в результате вычислений получено hу/х = А; hx/y = В. Если А > В то признак y зависит от x больше, чем x от y. Следовательно признак x доминирует. Если В > A, то x зависит от y больше, чем y от x, и признак y доминирует.
Пример 5.3.1. Упражнения А и В выполняются для развития ловкости. Предполагается, что между временем исполнения упражнения А и В существует связь. Восемь спортсменов (табл. 5.3.1) при исполнении упражнения А (xi) и В (yi) показали время (в секундах) – см. первые два столбца нижеприведенной таблицы. Определить корреляционные отношения hу/х; hx/y
Таблица 5.3.1
| хі | уі | 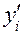
| 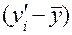
| 
| 
| 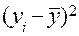
|
| 3,0 | 7,0 | 10,6 | —4,3 | -7,9 | 18,49 | 62,41 |
| 3.0 | 10,0 | 10,6 | —4,3 | —4,9 | 18,49 | 24,01 |
| 3,0 | 15,0 | 10,6 | —4.3 | +0,1 | 18,49 | 0,01 |
| 5,0 | 12,0 | 12,0 | —2,9 | —2,9 | 8.41 | 8,41 |
| 8,0 | 18,0 | 18,5 | +3,6 | +3,1 | 12,96 | 9,61 |
| 8,0 | 19,0 | 18,5 | 43,6 | +4,1 | 12,96 | 16,81 |
| 12,0 | 19,0 | 19,0 | +4,1 | +4,1 | 16,81 | 16,81 |
| 12,0 | 19,0 | 19,0 | +4,1 | +4,1 | 16,81 | 16,81 |
| 54,0 | 119,0 | 123,32 | 154,88 |
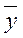 =
= 
На основании этой таблицы в соответствии с формулой (5.3.1) находим

Зависимость признака у от х весьма высокая.
Для вычисления корреляционного отношения hx/y исходные данные переписываем в табл. 5.3.2, выдвигая на первое место признак yi.
Таблица 5.3.2
| уі | хі | 
| 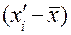
| 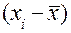
| 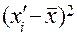
| 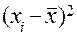
|
| 7,0 | 3,0 | 3,0 | —3,8 | -3,8 | 14,44 | 14,44 |
| 10,0 | 3,0 | 3,0 | —3,8 | —3,8 | 14,44 | 14,44 |
| 15,0 | 3,0 | 3,0 | —3,8 | -3,8 | !4,44 | 14,44 |
| 12,0 | 5,0 | 5,0 | —1,8 | —1,8 | 3,24 | 3,24 |
| 18,0 | 8,0 | 8,0 | +1,2 | +1,2 | 1,44 | 1,44 |
| 19,0 | 8,0 | 10,7 | +3,9 | +1,2 | 15,21 | 1,44 |
| 19,0 | 12,0 | 10,7 | +3,9 | +5,2 | 15,21 | 27,04 |
| 19,0 | 12,0 | 10,7 | +3,9 | +5,2 | 15,21 | 27,04 |
| 119,0 | 54,0 | 93,63 | 103,52 |
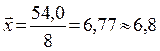
На основании этой таблицы по формуле (5.3.2) находим;
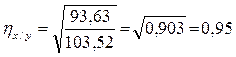
Оба корреляционных отношения не равны между собой, то есть первый признак от второго зависит не так, как второй от первого. При этом связь между признаками весьма тесная.
В обеих таблицах третьи столбцы посвящены определению частных средних  и
и 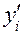 .
.
Так, в таблице 5.3.1 величина 10,6 найдена как средняя арифметическая величин 7,0; 10,0; 15,0, соответствующих трем одинаковым значениям (3,0) признака х, и т. д.
Дата добавления: 2015-10-24; просмотров: 130 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Графическое отражение корреляционной связи | | | Ранговая корреляция |