Вычислить коэффициент корреляции и оценить его значимость по критерию Стьюдента

КОНТРОЛЬНАЯ РАБОТА

По дисциплине:

ЭКОНОМЕТРИКА

Вариант № 8

Выполнил: студент гр. 201 ЭТ

Поселенцева Г.Д.

Проверил: преподаватель

Козий В.Ф.

Котельники -2013

ВАРИАНТ № 8

х	9,7	8,4		9,9	9,6	8,6	12,5	7,6	6,9	13,5
у	0,26	0,28	0,31	0,4	0,29	0,3	0,29	0,2	0,24	0,31

1. Вычислить коэффициент корреляции и оценить его значимость по критерию Стьюдента;

2. Построить линию регрессии и оценить влияние факторного признака на результативный признак с помощью коэффициента эластичности и β – коэффициента;

3. Проверить значимость коэффициента регрессии по критерию Стьюдента и доверительному интервалу;

4. Проверить значимость уравнения регрессии по критерию Фишера;

5. Оценить качество регрессионной модели по коэффициенту детерминации;

6. Проверить точность уравнения регрессии по средней ошибки аппроксимации.

Вычислить коэффициент корреляции и оценить его значимость по критерию Стьюдента

Для решения задач экономического анализа и прогнозирования очень часто используются статистические, отчетные или наблюдаемые данные. При этом полагают, эти данные являются значениями случайной величины.

Случайной величиной называется переменная величина, которая в зависимости от случая принимает различные значения с некоторой вероятностью. Закон распределения случайной величины показывает частоту ее тех или иных значений в общей их совокупности.

При исследовании взаимосвязей между экономическими показателями на основе статистических данных часто между ними наблюдается стохастическая зависимость. Она проявляется в том, что изменение закона распределения одной случайной величины происходит под влиянием изменения другой. Взаимосвязь между величинами происходит под влиянием изменения другой. Взаимосвязь между величинами может быть полной (функциональной) и неполной (искаженной другими факторами).

Пример функциональной зависимости выпуск продукции и ее потребление в условиях дефицита.

Неполная зависимость наблюдается, например, между стажем рабочих и их производительностью труда. Обычно рабочие с большим стажем трудятся лучше молодых, но под влиянием дополнительных факторов образование, здоровье и т.д. эта зависимость может быть искажена

Раздел математической статистики, посвященный изучению взаимосвязей между случайными величинами, называется корреляционным анализом (от латинского слова “correlatio” – соотношение, соответствие). Основная задача корреляционного анализа это установление характера и тесноты связи между результативными (значимыми) и факторными (независимыми) признаками в данном явлении или процессе. Корреляционную связь можно обнаружить только при массовом сопоставлении фактов.

Характер связи между показателями определяется по корреляционному полю. Если Y- результативный признак, а X- факторный, то, отметив каждый случай X_i с координатами X_i и Y_i, получим корреляционное поле. По расположению точек можно судить о характере связи (рис.1).

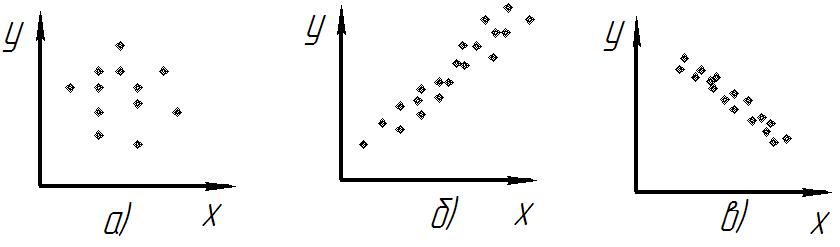
а) – переменные X и Y не коррелируют; б) – наблюдается сильная положительная корреляция; в) – наблюдается слабая отрицательная корреляция.

Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической взаимосвязи – например для независимых случайных величин). Отрицательная корреляция – корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции отрицателен. Положительная корреляция – корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции положителен.

Корреляция – статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.

С помощью коэффициента корреляции определяется теснота связи двух случайных величин. Он рассчитывается специальным образом и лежит в интервалах от минус единицы до плюс единицы. Если значение коэффициента корреляции лежит в интервале от 0,7 до 1 по модулю, то отмечается очень сильная корреляционная зависимость, от 0,5 до 0,7 – средняя корреляционная зависимость. В случае, если значение коэффициента корреляции лежит в интервале от 0,3 до 0,5, то говорят, что имеет место слабая корреляционная зависимость. Если значение коэффициента корреляции находится в интервале от 0 до 0,3, говорят об очень слабой корреляционной зависимости или полном ее отсутствии.

Таким образом, корреляционный анализ применяется для нахождения характера и тесноты связи между случайными величинами.

Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие.

Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.

Автокорреляция - статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса - со сдвигом по времени.

Ковариация – (от анг. “covariation” - “ совместная” вариация) – мера линейной зависимости двух величин.

Ковариация несет тот же смысл, что и коэффициент корреляции – она показывает, есть ли линейная зависимость между двумя случайными величинами, и может рассматриваться как «двумерная дисперсия». Однако, в отличие от коэффициента корреляции, который меняется от -1 до 1, ковариация не инвариантна относительно масштаба, т.е. зависит от единицы измерения и масштаба случайных величин.

Знак ковариации указывает на вид линейной связи между рассматриваемыми величинами: если она больше нуля то это означает прямую связь (при росте одной величины растет и другая), ковариация меньше нуля указывает на обратную связь. При ковариации равной нулю линейная связь между переменными отсутствует.

Пусть X и Y – две случайные величины, определенные на одном на одном и том же вероятностном пространстве. Тогда их ковариация определяется следующим образом:

cov(x,у) = М [ (X-m_x) (Y-m_y) ],

в предположении, что все математические ожидания М в правойчасти определены. Ковариация – промежуточное звено к определению коэффициента корреляции, т.к. коэффициент корреляции – это отношение ковариации к произведению среднеквадратических отклонений зависимой и независимой переменных.

сov(x,у) = ,

где cov (х,у) –ковариация;

n - объем выборки;

х_i – i - тое значение независимой переменной;

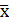– среднее значение независимой переменной;

у – среднее значение зависимой переменной.

Расчетная формула для вычисления коэффициента корреляции:

Расчетные формулы для вычисления средних значений зависимой и независимой переменной:

; ;

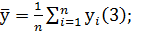
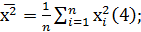
1.1 Пусть в таблице задана выборка значений случайных величин результативного признака Y и факторного признака Х

Предположим, что между X и Y существует линейная взаимосвязь, т.е. у=a+bx.

Для того, чтобы найти уравнение регрессии, прежде всего нужно исследовать тесноту связи между случайными величинами X и Y, т.е корреляционную зависимость.

Пусть x₁, x₂,…, x_n – совокупность независимого, факторного признака;

y₁, у₂,…,у_n - совокупность соответствующих значений независимого, результативного признака;

n – количество наблюдений.

Дата добавления: 2015-10-28