Оценка значимости коэффициента корреляции

Для оценки коэффициента корреляции используют критерий Стьюдента, который задан в таблице критических значений t-статистики Стьюдента. В этом случае выдвигается и проверяется основная гипотеза H₀ о равенстве коэффициента корреляции нулю:

основная гипотеза Н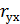₀: =0

конкурирующая гипотеза Н₁: 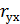≠0.

Если основная гипотеза отвергается, то коэффициент корреляции признается значимым, а связь между зависимой и независимой переменной-существенной.

Статистическая гипотеза – гипотеза о виде неизвестного распределения или параметрах известного распределения. Существует два вида гипотез: основная или нулевая (Н₀) и конкурирующая или альтернативная (Н₁). Для оценки гипотез используют ошибку первого рода, т.е. отвергается правильная гипотеза, и ошибку второго рода, т.е. принята неправильная гипотеза.

1.4.1 Вычислим t_расч. по формуле;

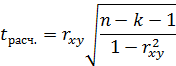
где

n - объем выборки;

k – число факторных признаков. Для парной регрессии факторный признак k=1.

1.4.2 Определяем t-табличное по Стьюденту:

tтб(α;df), где df –число степеней свободы;

α – уровень значимости.

Уровень значимости – вероятность совершить ошибку первого рода - α=0,05 (в пяти случаях из 100 существует риск допустить ошибку первого рода, т.е. отвергнута правильная гипотеза).

Число степеней свободы (разность между числом выборки и числом неизвестных параметров) определяем по формуле:

df=n-k-1=10-1-1= 8

t_тб=(α;df) = t_кр(0,05; 13) = 2,3060~2,31

1.5.3 Сравниваем t_{расчетное} и t_{табличное}:

- если t_расч>t_тб, то коэффициент корреляции признается значимым, т.е. основная гипотеза отвергается;

- если t_расч<t_тб, то коэффициент корреляции признается незначимым и основная гипотеза принимается.

Вывод: так как t_расч<t_тб коэффициент корреляции признается незначимым и основная гипотеза принимается.

2. Построить линию регрессии и оценить влияние факторного признака на результативный признак с помощью коэффициента эластичности и β – коэффициента

Регрессионный анализ своей целью имеет вывод, определение (идентификацию) уравнения регрессии, включая статистическую оценку его параметров. Уравнение регрессии позволяет найти значение зависимой переменной, если величина независимой переменной или независимых переменных известна. Уравнением регрессии называют функцию f(x), описывающую линию регрессии. Уравнения регрессии классифицируют на линейные (корреляционные) и нелинейные.

Практически, речь идет о том, чтобы, анализируя множество точек на графике (т.е. множество статистических данных), найти линию, по возможности точно отражающую заключенную в этом множестве закономерность (тренд, тенденцию), линию регрессии.

По числу факторов различают одно-, двух- и многофакторные уравнения регрессии.

По характеру связи однофакторные уравнения регрессии подразделяются:

а) на линейные: у=а+bx;

б) степенные: у=а ;

в) показательные: у=а ;

г) прочие.

Общий вид уравнения регрессии:

где а и б – параметры модели;

- случайная величина или величина остатка.

Параметр а – сводный коэффициент уравнения регрессии, не имеющий экономического смысла. Он показывает значение результативного признака у, если факторный признак х равен нулю (у=а, если х=0).

Параметр b – коэффициент регрессии. Он показывает, на какую величину в среднем изменится результативный признак у_х, если переменную х увеличить на единицу измерения. Знак коэффициента регрессии совпадает со знаком коэффициента линейной корреляции и показывает направление связи:

-если b>0 – линейная связь прямая;

- если b<0 – то линейная связь обратная;

- если b=0 – линейная связь между переменными отсутствует (линия регрессии параллельна оси абсцисс).

Величина ε – независимая нормально распределенная величина. Остаток с нулевым математическим ожиданием равен нулю (М_х=0), а дисперсия постоянна (D_Ɛ=сonst). Величина ε отражает тот факт, что изменение у будет не точно описываться изменением величины х, так как присутствуют другие факторы, не учтенные в данной модели.

Для оценки параметров a и b используют метод наименьших квадратов. Сущность МНК заключается в том, что отыскиваются такие значения параметров модели а и b, при которых сумма квадратов отклонений фактических значений результативного признака y_i от вычисленных по уравнению регрессии будет наименьшим из всех возможных:

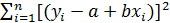= → min

Это означает, что вертикальное расстояние между точкой А_i(x_i:у_i) и соответствующей точкой на прямой должно быть наименьшим.

Формула для определения значений a и b

а = (10)

Дата добавления: 2015-10-28