Элементы комбинаторики

Из определенного числа элементов можно составлять сочетания, перестановки и размещения. Для того чтобы их вычислить, необходимо иметь представление о понятии факториала. Символически запись такая n! (читается: эн—факториал).

Факториал есть произведение натурального ряда чисел от 1 до n.

Например,

3!=1 •2 •3=6

5!=2 •3 •4 •5=120

7!==1•2 •3 •4 •5 •6 •7=5040 и т. д.

n!=1•2• 3• 4• 5•...... • n

Сочетание —это такая группа элементов, когда из большего их числа выбираем меньшее. Большее их число обозначим — n, меньшее — k. Вычисление сочетаний следует производить по формуле:

(3.1.1)

где 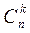— число сочетаний из n по k; n — все рассматриваемые элементы; k — меньшее их число.

Пример 3.1.1. Для упражнений с мячом необходимо отобрать 3 мяча из 5 имеющихся. Сколько возможных вариантов такого отбора?

Для определения количества вариантов необходимо найти число сочетаний (3 из 5), при этом большее число n =5, меньшее k =3.

В соответствии с формулой (3.1.1)

Пример 3.1.2. В тренировочном процессе можно использовать 50 различных физических упражнений. В одном занятии применяют 10. Сколько возможно получить вариантов занятий, не повторяющих друг друга?

Для определения количества занятий найдем число сочетаний из n = 50 по k = 10.

Перестановки – это образование таких групп элементов, когда общее их количество не меняется, а изменяется порядок их расположения. Перестановки элементов находятся по формуле:

P_k = k! (3.1.2)

где k – число всех элементов; Р – число перестановок из k элементов.

Пример 3.1.3. Сколькими способами могут быть расположены 6 игроков на волейбольном поле?

Общее количество игроков – 6. Число перестановок находим по формуле (3.1.2):

Р₆ = 6!=1 2 3 4 5 6=720.

Пример 3.1.4. Жребий определяет последовательность выступлений 10 спортсменов. Сколько вообще возможно способов в последовательности их выступлений?

Общее количество спортсменов – 10. Число перестановок находим по формуле (3.1.2):

Р₁₀ = 10! = 1 2 3 4 5 6 7 8 9 10=3 628 800.

Размещения – такая группа элементов, когда из большего числа n выбирается их меньшее число k, внутри которых производят перестановки.

Размещения вычисляют по формуле:

(3.1.3)

где – число размещений элементов из общего числа n по меньшему числу k; n – общее число элементов; k – меньшее число элементов.

Пример 3.1.5. Из 6 тренировок, идущих в последовательности 1, 2, 3, 4, 5, 6, три отведены для занятий гимнастикой. Это могут быть занятия 1, 2, 3 или 1, 4, 5, или 3, 4, 6 и т. д. Последовательность занятий гимнастикой также имеет значение. Среди избранных трех занятий 1, 2, 3 это может 1, 2, 3 или 2, 1, 3, или 3, 1, 2, и т. д. Сколько возможно получить вариантов для образования последовательности трех занятий гимнастикой с перестановкой их из 3 возможных?

Для определения количества вариантов находим число размещений из 6 по 3:

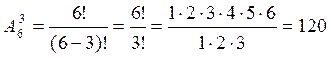
3.2. Теория вероятностей. Элементы теории вероятностей

Здесь будет рассмотрено понятие вероятности, лежащее в основе, как теории вероятностей, так и математической статистики.

Когда мы говорим о происхождении какого-либо случайного события, то всегда подразумеваем большую или меньшую возможность этого. Выпадение снега, например, событие случайное и появление его абсолютно точно предвосхитить нельзя. Однако, возможность появления его зимой очень велика, а появление его летом — почти невероятно. Таким образом, появление какого-либо случайного события в каких-либо определенных условиях имеет различную возможность.

Вероятность есть число, характеризующее возможность осуществления случайного события в определенном испытании.

Под испытанием подразумеваем, условия или обстоятельства, при которых осуществляется появление данного события.

В проведенной серии испытаний подсчитывают:

1) количество испытаний, имеющих благоприятный для целей задачи исход, то есть количество испытаний, в которых нужное нам событие появилось. Обозначим их число буквой m;

2) количество всех испытаний, имевших место в данной серии. Предполагается, что любой исход этих испытаний не имеет преимуществ перед остальными, т. е. все исходы имеют равные возможности для того, чтобы произойти. Эти исходы испытания называются равновозможными. Обозначим их n.

Вероятность появления случайного события в данном испытании есть частное от деления числа благоприятствующих исходов испытаний (m) на равновозможные (n).

Формула вероятности будет выглядеть следующим образом:

, (3.2.1)

где Р(А) —вероятность появления события А в данном испытании; m — количество благоприятствующих исходов испытания; n —количество равновозможных исходов испытаний.

Рассмотрим это на конкретном примере.

Пример 3.2.1. Конечной целью серии тренировок пловца является преодоление им дистанции 200 м вольным стилем за время 2.17,0.

После соответствующей подготовки он проплывал эту дистанцию 25 раз. Результаты его такие: 18 раз он показал желаемый результат, в остальных случаях — результат был хуже. Какова вероятность того, что в тех же условиях он преодолеет дистанцию 200 м за нужное время — 2.17,0?

Обозначим вероятность искомого случайного события буквой А. Определению подлежит вероятность Р(А). Используем формулу (3.2.1).

В данном примере благоприятствующих исходов испытаний было 18, то есть m =18. Равновозможные исходы испытания — это все испытания, имевшие место в данном примере. Их число n =25.

Таким образом, вероятность искомого события находится так:

Р(А) = 0,72 — есть числовая характеристика того, что в данном испытании спортсмен преодолеет дистанцию 200 м за 2.17,0.

Вероятность обычно выражается десятичной дробью. В некоторых случаях ее переводят в проценты, для чего полученную десятичную дробь следует умножить на 100%. В данном примере Р(А) = 0,72.100%=72%.

Вероятность еще можно трактовать как степень уверенности в том, что в данном испытании рассматриваемое случайное событие произойдет.

Пример 3.2.2. Спортсмен выполняет тройной прыжок, желая достичь результат 14,50 м. Из 20 прыжков в 12 он показал 14,50 м. Какова вероятность того, что на соревнованиях спортсмен достигнет желаемого результата?

m – число благоприятствующих исходов испытаний, m = 12, n – равновозможные исходы, n = 20. Вероятность удачи:

Р(А)= =

В соответствии с определением, вероятность, как число, определяется после того, как прошла серия испытаний. Имеется в виду тот факт, что в серии испытаний, которые еще не проведены, но будут иметь место, найденная вероятность появления случайного события будет та же, если будут соблюдены те же условия, что в прошедшей серии испытаний.

Рассмотрим два крайних условия: 1) если число всех благоприятствующих исходов равно числу всех равновозможных – т = п и 2) если благоприятствующих исходов не было – m = 0 — и все испытания есть равновозможные.

В примере 3.2.1 эти два крайние условия выглядят так:

1) проведено n = 25 испытаний и все 25 оказались удачными m = 25 (во всех 25 испытаниях он показал желаемый результат 2.17,0). В этом случае вероятность Р(А) есть:

Р(А)= =

Как видно из этого примера, более чем Р(А)=1 получить числа нельзя, т. к. m не может быть более чем 25.

Таким образом, мы получили одно крайнее условие: если m = n, то Р(А) = 1 и выше этого числа оно быть не может.

События, вероятность которых равна единице, называются достоверными в том смысле, что в данном испытании они должны произойти обязательно;

2) произведено n =25 испытаний и ни одно из них не оказалось удачным m = 0 (спортсмен ни разу не преодолел дистанцию за время 2.17,0, а показывал результаты хуже). В этом случае искомая вероятность есть:

Р(А)= =

Меньше числа 0 вероятность быть не может, так как рассмотрены уже все испытания и ни одно не удалось.

События, вероятность которых равна нулю, называются невозможными в том смысле, что в данном испытании они никогда не произойдут.

Таким образом, в крайних положениях вероятность равна нулю и единице. Во всех прочих случаях она будет принимать значения между нулем и единицей. Записывают это так:

, (3.2.2)

то есть значение вероятности колеблется в пределах от нуля до единицы.

Дата добавления: 2015-10-24