Ранговая корреляция

Наименование корреляции «ранговая» связано с понятием «ранг», то есть имеющий порядковый номер.

В некоторых случаях невозможно определить значения признаков. Например, не поддаются количественному выражению некоторые показатели педагогических, психологических, медицинских, спортивных исследований.

Вместе с тем можно установить последовательность этих показателей, положив в основу такого анализа какой-либо критерий.

Например, невозможно определить комплексную характеристику ведения боя у боксеров, однако можно установить последовательность в оценке боксеров, исходя из количества выигранных боев. Этот же пример можно отнести к гимнастам, фигуристам, игровикам и т. д.

Во всех этих случаях корреляционную связь между признаками можно оценить при помощи коэффициента ранговой корреляции R. Поскольку в основу его вычисления положены значения последовательности расположения объектов, а не значения собственно признаков, теснота связи улавливается слабее и точность исследований снижается.

К числу преимуществ этого метода следует отнести возможность работы с небольшим количеством объектов — в некоторых исследованиях это имеет очень большое значение.

Коэффициент ранговой корреляции можно определить по такой формуле:

(5.4.1)

где R —коэффициент ранговой корреляции; d —разность рангов, т. е. порядковых номеров объектов; n — количество исследуемых объектов.

Коэффициент ранговой корреляции изменяется от 0 до 1 и в соответствии с этим интервалом оценивается теснота искомой связи. Выводы по ранговому коэффициенту корреляции— те же, что и в вышеописанных коэффициентах.

Пример 5.4.1. Выступая на соревнованиях по II юношескому разряду, 7 гимнасток после выполнения упражнений на брусьях заняли такие места х_i. Эти же спортсменки при выполнении упражнений на бревне заняли места y_{i . (}таблица 5.4.1). Определить наличие корреляционной связи у исследуемых гимнасток по этим двум видам гимнастического многоборья.

Определяем коэффициент ранговой корреляции в соответствии с формулой (5.4.1):

Таблица 5.4.1

xi	yi	di = (xi-yi)	di^2
		—3
		—1
		+2
		– 3
		—1
		+1
		+5

n = 7

(n – 1) = 7 – 1 = 6

(n + 1) = 7 + 1 = 8

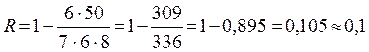
Коэффициент ранговой корреляции R=0,1 указывает на то, что у исследуемых 7 гимнасток почти отсутствует связь между результатами выполнения упражнений на брусьях и на бревне.

Приложение

Образец отчета о самостоятельной работе

Расчет основных статистических характеристик выборки:

Пример 1. У 34 спортсменов-лыжников зарегистрировано такое время восстановления пульса после прохождения дистанции (в секундах):

81; 78: 84; 90; 78; 74; 84; 85; 81; 84: 79; 84; 74; 84; 84;

85; 81; 84; 78: 81; 74; 84; 81; 84; 85; 81; 78; 81; 81; 84;

84; 84; 78; 81.

xi	ni	xini	xi-	|xi- |	|xi- |ni	(xi- )^2	(xi- )^2ni
			-7
			-3
			+3
			+4
			+9
	n=34

Графическое представление вариационного ряда

Среднее арифметическое ;

Среднее линейное отклонение ;

Дисперсия ;

Среднее квадратическое отклонение ;

Коэффициент вариации ;

Мода Mo = 84c;

Медиана Me = 81c.

Характеристика выборки: (81±2,9) или (81±3,6), V=4.5%, Mo = 84c, Me = 81c.

Пример 2. В течение серии тренировок спортсмен показал такую разность между временем бега на 800 м, деленным на 8, и временем бега на 100 м (х_i). Результат представлен в секундах.

xi	ni	xini	xi-	(xi- )^2	(xi- )^2ni	mi
6,00		42,00	+1,00	1.00	7,00
5,00		20,00 ^и,ци
4,50 3,80		9,00 11,40	-0,50 -1,20	0,25 1,44	0,50 4,32
3,50		3,50	-1,50	2,25	2,25
	n =17	85,90			14,07

Графическое представление вариационного ряда:

Среднее арифметическое ;

Дисперсия ;

Среднее квадратическое отклонение ;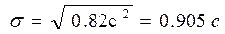

Коэффициент вариации ;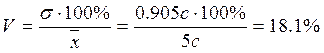

Мода Mo = 6c;

Медиана Me = 5c.

Характеристика выборки: V=18,1%, Mo = 6c, Me = 5c.

Содержание

Предисловие..................................................

1. Составление вариационных рядов их графическое представление

2. Параметры вариационных рядов..............

2.1 Мода.........................................................

2.2 Медиана...................................................

2.3 Среднее арифметическое.........................

2.4 Среднее квадратическое отклонение. Дисперсия..................................................

2.5 Коэффициент вариации...........................

Основные понятия теории вероятностей, комбинаторика. Нормальный закон распределения

3.1. Теория вероятностей…………………………………………

3.2. Основы комбинаторики……………………………………...

3.3. Нормальный закон распределения…………………………

4. Репрезентативность выборочных показателей

4.1.Ошибки репрезентативности..................

4.2.Критерий надежности……………………..

4.3. Достоверность различия между двумя выборочными средними……………………

5. Корреляция

Дата добавления: 2015-10-24