|
Читайте также: |
Предположим, что на основе геометрических или других соображений установлено, что между двумя количественными признаками 
и 
существует линейная корреляционная зависимость. Если признаки подчиняются нормальному закону распределения, то уравнение линии регрессии записывают в виде
(43)
Пусть опытные данные не сгруппированы в корреляционную таблицу, то есть заданы в виде табл. 18.
| Таблица 18 | |||||
| 
| 
| 
| … | 
|
| 
| 
| 
| … | 
|
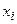
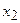
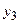
В этом случае значения 
и 
, являющиеся оценками истинных величин уравнения регрессии, находят по методу наименьших квадратов, решая систему нормальных уравнений
, (44)
где 
, 
, 
, 
.
Для нахождения сумм, входящих в систему (44) составляется табл. 19.
| Таблица 19 | |||
|
|
| 
| 
|
| 
| 
| 
|
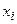
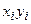
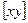
Если опытные данные сгруппированы в корреляционную таблицу, то значения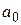 
и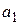 
уравнения регрессии (43) находят по методу наименьших квадратов, решая систему нормальных уравнений
, (45)
где 
и 
— частоты признаков и , 
— частота совместного появления признаков и .
Для нахождения сумм, входящих в систему (45) составляется табл. 20.
| Таблица 20 | ||||||
| x y |
|
| … |
| 
| 
|
| … | |||||
|
| … | |||||
| … | … | … | … | … | … | … |
| … | |||||
| … | 
| ||||
| … | 
| ||||
| … | 
| ||||
| … | 
|
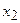
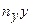
Суммы 
, 
, 
в табл. 20 находятся по строкам, а сумма 
находится по последнему столбцу табл. 20.
В уравнении регрессии (43) параметр 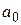характеризуют усредненное влияние на результативный признак неучтенных (не выявленных для исследования) факторных признаков 
. Параметр 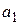показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного признака на единицу.
Используя параметр 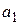, вычисляют коэффициент эластичности 
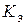по формуле
(46)
Коэффициент эластичности 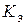показывает на сколько изменяется в процентах результативный признак при изменении факторного признака на 1 %.
В случае линейной корреляционной зависимости между признаками и , если нет уверенности в том, что эти признаки подчиняются нормальному закону распределения, уравнения линий регрессий находят по формулам:
, (47)
, (48)
где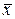 
, 
— выборочные средние признаков и ; 
, 
— выборочные средние квадратические отклонения признаков и , вычисляемые по формулам:
, где 
, (49)
, где 
. (50)
При 
и находят по формулам:
, где 
, (51)
, где 
. (52)
Коэффициент линейной корреляции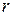 
находят по формуле
, (53)
где 
— средняя произведения значений признаков и , , 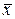— средние значения признаков и , , — выборочные средние квадратические отклонения признаков и , вычисленные по формулам (49) и (50), если 
или по формулам (51) и (52), если .
Уравнение (47) называют уравнением регрессии 
на 
, а уравнение (48) — уравнением регрессии на .
Если данные выборки для признаков и заданы в виде корреляционной таблицы и объем выборки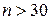 
, то для нахождения величин, входящих в уравнения линий регрессий (47) и (48), переходят к вспомогательному распределению с условными вариантами 
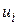и 
, вычисляемых по формулам:
, (54)
, (55)
где 
, 
, 
и 
— шаги значений признаков и .
Выборочный коэффициент линейной корреляции 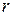в этом случае находят по формуле
, (56)
где
, 
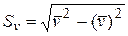(57)
Для нахождения суммы 
составляется расчетная табл. 21.
| Таблица 21 | |||||
| 
| 
| … | 
| 
|
| 
| 
| … | 
| 
|
| 
| 
| … | 
| 
|
| … | … | … | … | … | … |
| 
| 
| … | 
| 
|
| 
| 
| … | 
| 
|
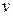
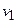
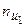
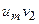
Статистики 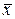, , , находят по формулам:
, 
, 
, 
. (58)
Дата добавления: 2015-10-29; просмотров: 107 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задачи теории корреляции | | | Линейного однофакторного уравнения |