Множественная регрессия

Производственные взаимосвязи, как правило, определяются большим числом одновременно и совокупно действующих факторов. Например, овальность после чистового шлифования зависит от припуска на чистовое шлифование и от овальности после предварительного шлифования. Себестоимость продукции зависит от стоимости материала, основной зарплаты рабочих, премиальных, расходов на содержание оборудования, отчислений на соцстрахование. В связи с этим возникает задача исследования зависимости между факторными признаками (называемыми также регрессорами или предикторами) , ,..., 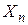и результативным признаком . Для этого используется множественный регрессионный анализ.

Построение многофакторной регрессионной модели начинается с установления формы связи, используя графический метод для пространства и метод перебора различных уравнений. От правильности выбора вида уравнения зависит, насколько построенная модель будет адекватна не только имеющимся экспериментальным данным, но и истинной зависимости между изучаемыми показателями. При прочих равных условиях предпочтение отдается модели, зависящей от меньшего числа параметров, так как для их оценки требуется меньшее количество эмпирических данных.

После выбора формы многофакторной регрессионной модели проводят отбор факторных признаков и включение их в модель. Принято считать, что в уравнение множественной регрессии можно включать только независимые друг от друга факторные признаки . Практически факторные признаки зависят либо слабо, либо сильно. Поэтому вопрос о включении факторных признаков в уравнение регрессии решает следующим образом. Пусть, например, имеется три факторных признака , , , 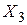влияющих на результативный признак и модель является линейной. Чтобы выяснить, какие факторные признаки включить в модель, находят коэффициенты парной корреляции , , . Если их значения меньше , то их можно включить в модель. Если же их значение больше , то следует какие-то из этих факторов исключить из модели. Пусть, например, . Ясно, что какой-то из признаков или 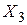надо исключить из модели. Для этого находят парные коэффициенты корреляции между каждым из факторов и и 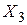результативным признаком , то есть вычисляют и . Затем сравнивают и . Пусть оказалось, что . Это означает, что факторный признак 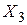сильнее связан с результативным признаком , чем признак . 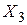Поэтому фактор следует включить в модель, а исключить из нее. Этот вывод подтверждаем путем вычисления коэффициентов частной корреляции и 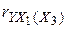. При исключении факторов из модели можно руководствоваться правилом. Если , где

, (89)

то один из факторов, либо , либо следует исключить.

Рассмотрим случай построения многофакторной модели, когда результативный признак зависит от двух факторных признаков и . Если зависимость между ними носит линейный характер, то уравнение регрессии записывают в виде

. (90)

Коэффициенты уравнения регрессии (90) , , находят по методу наименьших квадратов, решая систему нормальных уравнений

. (91)

Коэффициенты , , можно находить по формулам

, (92)

, (93)

. (94)

Здесь , , — коэффициенты парной корреляции между признаками и , и , и ; , , 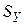— средние квадратические отклонения; , , — средние признаков , , .

Если уравнение линейной регрессии имеет вид

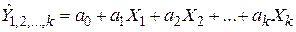(95)

то коэффициенты , , ,..., 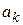находят решая систему нормальных уравнений

(96)

В матричной форме система (96) примет вид

(97)

где — матрица значений факторных признаков или матрица плана размерности 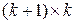; — транспортированная матрица ; — матрица коэффициентов системы нормальных уравнений (96) размерности ; — матрица-столбец значений результативного признака размерности ; — матрица-столбец свободных членов системы (97) размерности 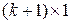. Для оценки надежности коэффициентов , , ,..., 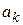находят средние квадратические ошибки этих коэффициентов, то есть находят 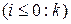. Пусть — матрица коэффициентов при переменных системы (97), обратная матрице . 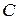Тогда средние квадрвтические ошибки коэффициентов вычисляют по формуле

(98)

где

, — диагональный элемент матрицы , соответствующий факторному признаку .

Пример.

По опытным данным найдены

,

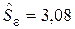и уравнение регрессии . Вычислить средние квадратические ошибки коэффициентов уравнения регрессии.

Воспользуемся формулой (98). Учитывая условие задачи, находим , , 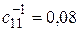, . Тогда

, ,

, .

Записываем уравнение регрессии и под коэффициентами их полученные ошибки:

(25,826) (0,871) (0,436) (0,533)

Дата добавления: 2015-10-29