Распределения. Рассмотрим выборку объема n со значениями признака Х:

Рассмотрим выборку объема n со значениями признака Х: 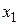, ,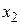..., . Для характеристики важнейших свойств статистического распределения используют средние показатели, называемые выборочными числовыми характеристиками. Если значения 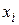признака Х не сгруппированы в вариационные ряды (табл. 2, 3, 4) и объем выборки n небольшой, то несмещенные оценки для неизвестных математического ожидания а и дисперсии находят по формулам:

(2)

для математического ожидания и

(3)

для дисперсии.

Если результаты наблюдений сгруппированы в дискретный вариационный ряд (табл. 3), то те же оценки находятся по формулам:

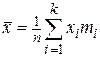, , 4)

, (5)

По формуле (5) вычисляют в случае, если объем выборки . Если же , то вычисляют исправленную дисперсию по формуле:

(6)

для простой выборки или

(7)

для взвешенной выборки.

Выборочное среднее квадратичное отклонение находят по формулам

или (8)

при различных объемах выборки.

Для анализа вариационных рядов вычисляют такие статистики, как моду и медиану.

Модой называют варианту, которая имеет наибольшую частоту. Например, для вариационного ряда

xi
mi

=9.

Медианой 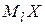называют варианту, которая делит вариационный ряд на равные части.

При нечетном объеме выборки (нечетном числе столбцов в дискретном вариационном ряде) медиана равна серединному члену вариационного ряда. Например, для вариационного ряда

xi
mi

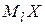=8.

При четном объеме выборки (четном числе столбцов в дискретном вариационном ряде) медиана находится по формуле

(9)

Здесь 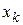— варианта, которая находится слева от середины вариационного ряда, а 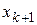— слева от нее. Например, для вариационного ряда

xi
mi

.

Для вычисления выборочной средней (), выборочной дисперсии (), асимметрии () и эксцесса (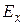) при достаточно большом объеме выборки () применяют метод произведений. Вводят условные варианты u_i, которые вычисляют по формуле

, (*)

где 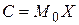, h — шаг (длина интервала).

Составляется расчетная табл. 6.

Таблица 6
							контрольный столбец
строка сумм:

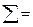
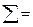
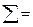
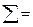
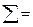
Контроль вычислений ведут по формуле

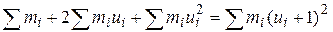. (10)

Пользуясь табл. 6, вычисляют условные начальные моменты по формулам

(11)

(12)

(13)

(14)

Тогда выборочную среднюю находят по формуле

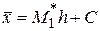(15)

Выборочную дисперсию находят по формуле

(16)

Выборочное среднее квадратическое отклонение находят по формуле

(17)

Асимметрию и эксцесс находят по формулам

(18)

, где (19)

— (20)

условный центральный момент третьего порядка, а

— (21)

условный центральный момент четвертого порядка.

Для характеристики колеблемости признака Х используют относительный показатель — коэффициент вариации V, который вычисляют по формуле

(22)

Дата добавления: 2015-10-29