Определение силы криволинейной связи

Для определения тесноты связи между признаками и при нелинейной корреляции используют корреляционные отношения и индекс корреляции.

Корреляционным отношением называется величина, определяемая равенством

(82)

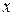где — объем выборки, — частота значения признака , — частота значения у признака , — общая средняя признака , — условная средняя признака .

Аналогично определяется выборочное корреляционное отношение

(83)

Корреляционные отношения обладают следующими свойствами (сформулируем свойства для , так как для , они аналогичны).

Корреляционное отношение заключено между 0 и 1, то есть

.

Если корреляционная связь между признаками и отсутствует, то и обратно.

Если , то между признаками и существует обычная функциональная связь.

Чем ближе значение к 1, тем сильнее корреляционная связь между признаками и , а чем ближе к 0, тем слабее эта зависимость.

Если регрессия на 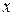является линейной.

Коэффициент линейной корреляции 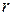не превосходит по модулю то есть .

По коэффициенту корреляции 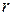можно судить о наличии и тесноте линейной корреляционной связи между признаками и . По корреляционным отношениям можно судить только о наличии и силе корреляционной связи между признаками и , но не о форме связи, которая устанавливается из геометрических соображений.

Теснота связи между признаками и при любой форме корреляции может быть измерена с помощью индекса корреляции . Если опытные данные не сгруппированы в корреляционную таблицу, то индекс корреляции находят по формуле

(84)

где — средний квадрат отклонений фактических значений от значений , вычисленных по уравнению регрессии; — средний квадрат отклонений фактических значений от их средней арифметической. Если опытные данные сгруппированы в корреляционную таблицу, то индекс корреляции находят по формуле

(85)

(86)

где , , ,

, .

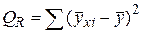Индекс корреляции по величине изменяется от 0 до 1. По индексу корреляции можно определять, как правило, тесноту связи между признаками и , но не обязательно форму криволинейной связи.

Дата добавления: 2015-10-29