Читайте также:
|
После проверки модельного уравнения линейной регрессии на адекватность находят относительную погрешность уравнения по формуле
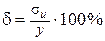, (67)
где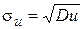 
, 
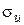— стандартная ошибка уравнения регрессии,
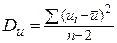— остаточная дисперсия,
, 
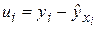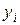— опытные значения 
, 
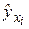— значения , полученные по уравнению регрессии, 
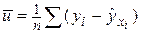— среднее значение 
, 
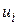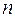— объем выборки.
Если величина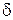 
мала, то прогнозные качества оценочного регрессивного уравнения высоки.
Одновременно производят оценку коэффициентов уравнения регрессии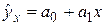 
. Пусть 
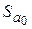и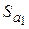 
— средние квадратические (или стандартные) ошибки соответственно коэффициентов 
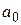и 
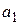уравнения регрессии. Их вычисление производят по формулам:
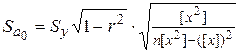(68)
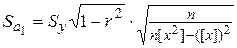(69)
Коэффициенты 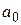и 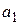считаются значимыми, есл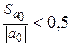и
и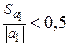 
.
Если коэффициенты 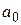и 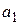незначимы, то ситуацию можно поправить путем увеличения объема выборки 
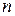, увеличения числа факторов, включаемых в модель или изменения формы уравнения связи.
Применения теории §§ 8-14 демонстрируется на примере выполнения лабораторных работ № 3 и № 4.
Контрольные вопросы
Дать определение корреляционной зависимости между двумя признаками 
и 
.
Дать определение условной средней признака и записать формулу для ее нахождения.
Сформулировать задачи, решаемые в теории корреляции.
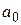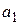Записать систему нормальных уравнений для нахождения параметров и уравнения линейной регрессии 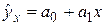в случае, когда опытные данные не сгруппированы в корреляционную таблицу.
Записать уравнения линий регрессий на 
и на , используя коэффициент линейной корреляции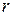 
.
Дать определение коэффициента линейной корреляции, сформулировать его свойства.
Рассказать о том, как определяется теснота линейной корреляционной связи между двумя признаками с помощью коэффициента линейной корреляции.
Как определяется значимость коэффициента линейной корреляции?
Записать доверительные интервалы для оценки коэффициента линейной корреляции при различных объемах выборки.
Записать формулу для нахождения коэффициента детерминации в случае парной линейной корреляции и рассказать о его назначении.
Рассказать о проверке адекватности уравнения линейной регрессии на для случая несгруппированных опытных данных.
Рассказать о нахождении относительной погрешности линейного уравнения регрессии .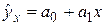
Как производится оценка коэффициента 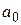и 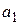уравнения линейной регрессии ?
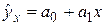Дата добавления: 2015-10-29; просмотров: 101 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Парная линейная корреляция | | | Для несгруппированных данных |