
Читайте также:
|
Между изучаемыми признаками  и
и  может существовать нелинейная корреляционная зависимости. Различают следующие виды нелинейной корреляции: параболическую, гиперболическую, экспоненциальную и другие.
может существовать нелинейная корреляционная зависимости. Различают следующие виды нелинейной корреляции: параболическую, гиперболическую, экспоненциальную и другие.
Путь зависимость между признаками  и
и  задана в виде корреляционной таблицы. Для определения типа нелинейной в системе координат на плоскости строят точки
задана в виде корреляционной таблицы. Для определения типа нелинейной в системе координат на плоскости строят точки  . Если точки в корреляционном поле располагаются вблизи некоторой параболы, то уравнение регрессии записывают в виде
. Если точки в корреляционном поле располагаются вблизи некоторой параболы, то уравнение регрессии записывают в виде
 . (72)
. (72)
Оценка 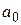 ,
,  ,
, 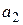 для неизвестных параметров истинного уравнения регрессии находят по методу наименьших квадратов. Если опытные данные не сгруппированы в корреляционную, то оценки находят, решая систему нормальных уравнений
для неизвестных параметров истинного уравнения регрессии находят по методу наименьших квадратов. Если опытные данные не сгруппированы в корреляционную, то оценки находят, решая систему нормальных уравнений
 (73)
(73)
Для сгруппированных значений признаков  и
и  оценки
оценки 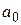 ,
,  ,
, 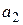 находят, решая систему, нормальных уравнений
находят, решая систему, нормальных уравнений
 (74)
(74)
Зависимость между  и
и  может быть близкой к гиперболической. В этом случае уравнение регрессии ищут в виде
может быть близкой к гиперболической. В этом случае уравнение регрессии ищут в виде
 (75)
(75)
Оценки 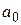 и
и  неизвестных параметров истинного уравнения регрессии находят по методу наименьших квадратов, решая систему нормальных уравнений
неизвестных параметров истинного уравнения регрессии находят по методу наименьших квадратов, решая систему нормальных уравнений
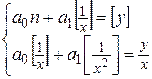 (76)
(76)
где  — сумма величин, обратных значениям
— сумма величин, обратных значениям  ,
,  сумма их квадратов,
сумма их квадратов, 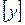 — сумма величин
— сумма величин  ,
, 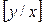 — сумма отношений значений
— сумма отношений значений  к
к  .
.
Если гиперболическая зависимость между признаками  и
и  имеет вид
имеет вид
 (77)
(77)
то оценки 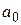 и
и  находят, решая систему нормальных уравнений
находят, решая систему нормальных уравнений
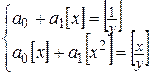 (78)
(78)
Если зависимость между признаками имеет экспоненциальный характер, то уравнение регрессии ищут в виде
 (79)
(79)
Для определения оценок  и
и  входящих в уравнение регрессии решают систему нормальных уравнений
входящих в уравнение регрессии решают систему нормальных уравнений
 (80)
(80)
Если в корреляционном поле около построенных точек предполагается проведение разных по типу линий (параболы, гиперболы, экспоненты, логарифмики), то для выбора одной из них, характеризующей наилучшим образом зависимость между признаками  и
и  , применяют либо метод конечных разностей, либо производят проверку необходимых условий.
, применяют либо метод конечных разностей, либо производят проверку необходимых условий.
Проверка необходимых условий
Проверку необходимых условий для выбора одной из предполагаемых нелинейных зависимостей проводят, пользуясь табл. 33.
| Таблица 33 | ||
| Необходимые условия | Вид формулы | Способ выравнивания (приведения к линейной зависимости) |

| 
| |
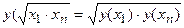
| 
|  , ,  , ,
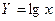 , ,  , , 
|

| 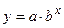
|  , ,  , ,
 , ,  , , 
|

| 
|  , ,  , , 
|

| 
|  , ,  , , 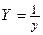
|

| 
|  , ,  , , 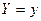
|
Если выполняется одно из условий первого столбца таблицы, то выбирают в качестве предполагаемой формулы соответствующую формулу, стоящую во втором столбце таблицы рассматриваемой строки. В третьем столбце указывается способ выравнивания, то есть приведения изучаемой зависимости к линейной. Если выравненные точки  хорошо ложатся на прямую, то указанную во втором столбец таблицы зависимость принимаем в качестве предполагаемой.
хорошо ложатся на прямую, то указанную во втором столбец таблицы зависимость принимаем в качестве предполагаемой.
Если значения функции, вычисленные в первом столбце таблицы при выбранных значениях аргумента отсутствуют в таблице опытных данных, то их находят линейным интерполированием по формуле
 , (81)
, (81)
где 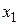 и
и  — два рядом стоящих значения признака
— два рядом стоящих значения признака  в таблице опытных данных, между которыми находится значение
в таблице опытных данных, между которыми находится значение 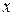 , вычисленное по табл. 33 первого столбца.
, вычисленное по табл. 33 первого столбца.
Для всех предполагаемых формул по результатам первого столбца табл. 33 вычисляют отклонения 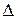 правой части от левой необходимого условия. Вычисленные отклонения
правой части от левой необходимого условия. Вычисленные отклонения  сравнивают и по наименьшему из них выбирают окончательно одну из формул.
сравнивают и по наименьшему из них выбирают окончательно одну из формул.
Метод конечных разностей.
Пусть в корреляционном поле могут быть проведены линии, описываемые уравнениями 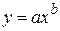 ,
, 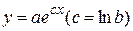 ,
,  ,
,  ,
,  . Все эти формулы содержат по два параметра и могут быть приведены к формуле
. Все эти формулы содержат по два параметра и могут быть приведены к формуле  , пользуясь таблицей 33. Так как все зависимости, приведенные в таблице 33, сводятся к линейной, то для обоснования выбора формулы
, пользуясь таблицей 33. Так как все зависимости, приведенные в таблице 33, сводятся к линейной, то для обоснования выбора формулы  вычисляют отношения
вычисляют отношения  ,
, 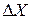 и
и 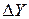 — конечные разности первого порядка. Аналитическим критерием выбора формулы по этому методу служит тот факт, что отношения
— конечные разности первого порядка. Аналитическим критерием выбора формулы по этому методу служит тот факт, что отношения  мало отличаются друг от друга для выбранной формулы.
мало отличаются друг от друга для выбранной формулы.
Если предполагаемая формула имеет вид  , то критерием выбора этой формулы являются незначительные отклонения по модулю конечных разностей второго порядка
, то критерием выбора этой формулы являются незначительные отклонения по модулю конечных разностей второго порядка  от среднего значения этих разностей
от среднего значения этих разностей  . Конечные разности находят, пользуясь табл. 34.
. Конечные разности находят, пользуясь табл. 34.
| Таблица 33 | |||
| Таблица конечных разностей | |||
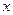
| 
| 
| 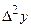
|

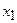
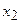


 …
…
| 
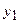



 …
…
| 
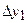


 …
…
| 


 …
…
|
Дата добавления: 2015-10-29; просмотров: 304 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Для несгруппированных данных | | | Определение силы криволинейной связи |