Первичная обработка результатов наблюдений

В первичной обработке результатов наблюдений при анализе показателей работы разных отраслей производственной сферы (добыча нефти и газа, ремонт скважин, машиностроение, строительная индустрия и т.д.) и их прогнозировании используют методы математической статистики, которые позволяют установить закономерности производственных результатов с требуемой точностью, надежностью и минимальных материальных, трудовых затратах и оценить их основные свойства.

Решение этих вопросов методами математической статистики осуществляют следующим образом.

Пусть Х — некоторый производственный показатель (признак), а 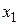, ,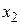..., 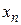— результаты независимых наблюдений над ними. Если количество наблюдений n невелико, наблюдения либо ранжируют, либо сводит в табл. 1, где каждому значению 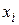ставят в соответствие частоту 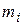появления этого значения в данной выборке.

Таблица 1
Варианты,			...
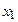
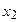
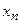
частоты,			...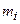

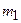
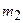
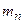
Здесь 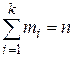, где n — объем выборки.

Если количество наблюдений n достаточно большое (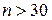), то результаты наблюдений сводят в интервальный вариационный ряд, который формируется следующим образом.

Вычисляют размах варьирования R признака Х, как разность между наибольшим 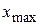и наименьшим 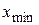значениями признака, то есть 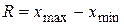. Размах R варьирования признака Х делится на k разных частей и таким образом определяется число столбцов (интервалов) в таблице. Величину k частичного интервала выбирают, пользуясь следующими правилами:

, , .

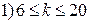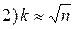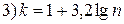При небольшом объеме n выборки число интервалов принимают равным от 6 до 10. Длина h каждого частичного интервала определяется по формуле

.

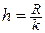Величину h обычно округляют до некоторого значения d. Например, если результаты 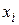признака Х — целые числа, то h округляют до целого значения, если 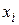содержат десятичные знаки, то h округляют до значения d, содержащего такое же число десятичных знаков. Затем подсчитывается частота 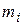, с которой попадают значения 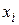признака Х в i -ый интервал. Значение 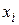, которое попадает на границу интервала относятся к какому-либо определенному концу, например, к левому. За начало 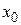первого интервала рекомендуется брать величину 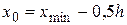. Конец 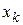последнего интервала находят по формуле 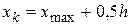. Сформированный интервальный вариационный ряд записывают в виде табл. 2.

Таблица 2
Варианты-интервалы, (; )	(; )	(; )	...	(; )
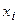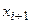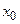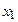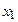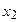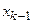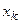частоты,			...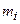

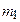
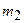
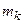
Интервальный вариационный ряд изображают геометрически в виде гистограммы частот 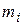или гистограммы относительных частот .

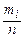Гистограммой называется ступенчатая фигура, для построения которой по оси 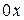откладывают отрезки, изображающие частичные интервалы (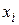; 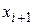) варьирования признака Х, и на этих отрезках, как на основаниях, строят прямоугольники с высотами, равными частотам или частостям соответствующих интервалов.

Для расчета статистик (выборочной средней, выборочной дисперсии, асимметрии и эксцесса) переходят от интервального вариационного ряда к дискретному. В качестве вариантов 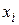этого ряда берут середины интервалов (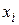; 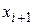). Дискретный вариационный ряд записывается в виде табл. 3 или табл. 4.

Таблица 3
Варианты, хi	х 1	х 2	...	хk
частоты, mi	m 1	m2	...	mk

Здесь 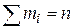, где n — объем выборки.

Таблица 4
Варианты,			...
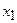
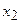
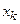
относительные частоты,			...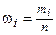

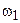
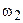
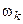
Здесь .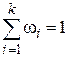

Графически дискретный вариационный ряд изображают в виде полигона частот или относительных частот. В системе координат 0 ху строят точки с координатами (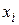; 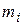) или (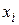; 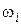), где 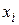— значение i -го варианта, а 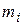(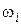) — соответствующие частоты (частости). Ломаную линию, соединяющую построенные точки, называют полигоном.

Вариационные ряды графически можно изобразить в виде кумулятивной кривой (кривой сумм — кумуляты). При построении кумуляты дискретного вариационного ряда на оси абсцисс откладывают варианты 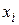, а по оси ординат соответствующие им накопленные частоты 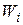. Соединяя точки с координатами (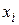; 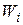) отрезками прямых, получаем ломаную (кривую), которую называют кумулятой. Для получения накопительных частот и дальнейшего построения точек (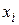; 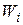) составляется расчетная табл. 5.

Таблица 5
Варианты,			...
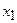
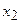
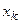
относительные частоты,			...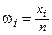
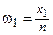
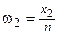
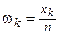
накопительные относительные частоты,			...

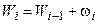
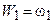
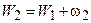
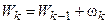
При построении кумуляты интервального вариационного ряда левому концу первого интервала соответствует частота, равная нулю, а правому — вся частота этого интервала. Правому концу второго интервала соответствует накопительная частота первых двух интервалов, то есть сумма частот этих интервалов и т. д. Правая граница последнего интервала равна сумме всех частот, то есть объему n выборки.

Для характеристики свойств статистического распределения в математической статистике вводится понятие эмпирической функции распределения.

Эмпирической функцией распределения или функцией распределения называется функция 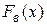, определяемая равенством

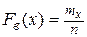, (1)

где n — объем выборки, 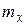— число вариантов 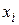, меньших х. Аналогом этой функции в теории вероятностей является интегральная функция распределения 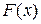. Функция 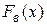отличается от функции 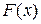тем, что вместо вероятности P (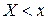) берется относительная частота .

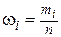Чтобы найти значение функции 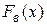приданном значении x, надо подсчитать число вариантов, которые принял признак Х меньше, чем х и разделить на объем выборки.

Эмпирическая функция 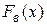служит для оценки теоретической функции распределения генеральной совокупности. При больших объемах n выборки согласно знака больших чисел функции 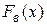сходится по вероятности к теоретической функции 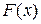признака Х.

Значения эмпирической функции 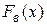принадлежат промежутку 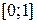. Графиком функции 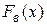служит кусочно-постоянная кривая (рис. 1).

Эта кривая имеет скачки в точках, которые соответствуют вариантам 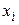. При обработке результатов эксперимента, например, результатов механических испытаний, целесообразно вместо ступенчатой кривой вычерчивать плавную кривую (на рис. 1 это штриховая линия), которая проходит через точки, расположенные посередине вертикальных частей ступенчатой кривой. Абсциссами этих точек служат значения механической характеристики 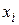, а ординатами — эмпирическая функция 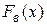, характеризующая оценку вероятности события .

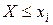Дата добавления: 2015-10-29