IV. Обработка результатов измерений

6. По формуле (1.11) вычислить g_i для каждого измерения.

7. Рассчитать среднее арифметическое значение <g>=Sg_i/N, где N – количество измерений.

8. Вычислить абсолютные погрешности каждого измерения по формуле Dg_i =<g> - g_i

9. Определить среднюю арифметическую случайную погрешность <Dg>=S½Dg_i ½/N.

10. Занести в таблицу конечный результат.

V. Вывод:

Показатель адиабаты для воздуха γ=<g>±Δg = …±…

Контрольные вопросы

1. Что называют термодинамической системой? Какие виды т-д систем различают?

2. Что называется внутренней энергией системы? Сформулируйте первое начало т-д.

3. Приведенная теплота и энтропия в обратимом и необратимом процессе. Второе начало термодинамики.

4. Термодинамическое и статистическое (вероятностное) толкование энтропии.

5. Принцип Пригожина.

6. Что называется теплоемкостью т-д системы? Теплоемкость при постоянном объеме и при постоянном давлении.

7. Уравнение Майера и физический смысл универсальной газо­вой постоянной.

8. Опишите установку, объясните происходящие при выполнении работы процессы и диаграмму Р-V состояния воздуха при этих процессах.

9. Что такое удельный объем газа?

10. Какой процесс называется адиабатическим? Почему его еще называют изоэнтропийным процессом?

11. Напишите уравнение Пуассона. Почему коэффициент Пуассона g >1?

ЛАБОРАТОРНАЯ РАБОТА №2 (1-15)

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ ПО МЕТОДУ СТОКСА

Цель работы: определение коэффициента динамической вязкости жидкости, а также числа Рейнольдса при движении в жидкости.

I. Описание установки. Приборы и принадлежности.

Жидкость налита в стеклянный цилиндрический сосуд, позволяющий наблюдать падение стального шарика в жидкости (см. рис.1.3). Для измерения скорости падения шарика потребуются: 1) секундомер; 2) измерительная шкала; 3) микрометр - для измерения диаметра шарика.

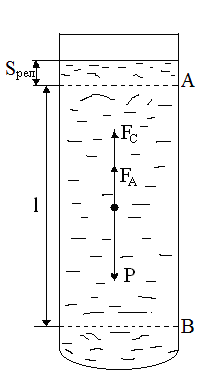
Рис. 2.1. Схема установки и силы, действующие на падающий шарик.

Прибор для определения коэффициента вязкости жидкости ме­тодом падающего шарика представляет собой высокий стеклянный цилиндр, наполненный исследуемой жидкостью. На наружной по­верхности цилиндра нанесены метки А и В на расстоянии l друг от друга (рис. 2.1), относительно которых фиксируется дви­жение падающего шарика. Верхняя метка располагается ниже уров­ня жидкости настолько, чтобы скорость шарика к моменту прохож­дения этой метки успевала установиться.

В качестве исследуемой жидкости выбран глицерин. Плотность глицерина 1,2×10³ кг/м³. В работе рассматривается падение в глицерине стального шарика; его плотность равна r_c = 7,8×10³ кг/м³.

II. Методика работы.

Свойство сред (жидкостей и газов) оказывать сопротивление движению в них инородных тел называется внутренним трением, или вязкостью. Это явление было изучено Исааком Ньютоном (1643-1727гг.) Вязкость проявляется в том, что при сдвиге соседних слоев среды относительно друг друга возникает сила противодействия – напряжение сдвига и, следовательно, сила сопротивления, которая для обычных сред пропорциональна величине скорости v относительного движения слоев. Коэффициент пропорциональности называется коэффициентом динамической вязкости, или просто вязкостью h среды.

Из закона вязкого трения Ньютонa следует, что

h = F / S(du/dx) (2.1)

Единица измерения вязкости в системе СИ: [h] = кг·м^-1·с^-1 = Па·с

В 1851г. английский физик и математик Джордж Габриель Стокс установил, что сила сопротивления, испытываемая твердым шаром при его медленном поступательном движении в неограниченной вязкой жидкости (в соответствии с законом вязкого трения Ньютона), прямо пропорциональна величине скорости v шарика, направлена навстречу движению v и описывается формулой, носящей имя Стокса:

F_с = 6p h r v, (2.2)

где r – радиус шарика.

На шарик, находящийся в сосуде с жидкостью, действуют следующие силы:

1) сила тяжести, направленная вниз, к центру Земли

F_т = mg =Vr_cg = pd³r_cg/6 (2.3)

2) выталкивающая сила Архимеда (ок. 287-212 до н.э.), направленная вверх

F_А = V r_гл g = pd³r_гл g/6 (2.4)

3) сила сопротивления жидкости (сила Стокса), также направленная вверх:

F_с = 3p h d v (2.5)

Здесь d – диаметр шарика, V - его объем, r_с и r_гл - плотности стали и глицерина соответственно, g = 9,81 м/с² – ускорение свободного падения.

При установившемся движении скорость шарика постоянна, т.е. ускорение его движения равно нулю, и, следовательно, по 2-му закону Ньютона, результирующая всех сил также равна нулю. С учетом знаков:

F _рез = Fс+ F_А - F_т = 0 (2.6)

Подставим в (2.6) выражения сил из (2.3), (2.4) и (2.5) и получим:

pd³ (r_c -r_гл) g/6=3p h d v,(2.7)

откуда коэффициент вязкости

h = d² (r_c -r_гл) g/18v (2.8)

Так как скорость v =l/t, где l - расстояние, пройденное шариком при установившемся движении за время t, то расчетная формула для определения коэффициента вязкости приобретает вид:

h = d² (r_c -r_гл) g t /18 l (2.9)

Здесь d, l, t – непосредственно измеряемые величины;

r_c и r_гл –берется из таблиц физических величин.

III. Порядок измерений и таблица результатов.

1. С помощью линейки измерить расстояние l между рисками А и В на мерной шкале, расположенной за стеклянным цилиндром.

2. С помощью микрометра измерить диаметр шарика d.

3. Осторожно опустить шарик сверху в глицерин примерно в центре сечения сосуда.

4. С помощью секундомера определить время t прохождения шарика между рисками А и В.

5. Результаты измерений занести в таблицу измерений.

6. Повторить измерения по пунктам 2¸5 еще с 4-мя шариками разных диаметров.

Таблица

№ опыта	l, см	d, мм	t, c	hi, Па×с	hср, Па×с	Dh,Па× с	Dhср, Па×с

IV. Обработка результатов измерений.

1. Рассчитать значения коэффициентов вязкости по формуле (2.9) для каждого опыта.

2. Определить среднее арифметическое значение вязкости:

h_ср =S |h_i |/n, где n = 5.

3. Определить отклонение Dh_i для каждого опыта: Dh_i = h_ср -h_i.

4. Рассчитать среднюю погрешность определения вязкости:

Dh_ср =SDh_i /n.

5. Рассчитанные значения занести в таблицу.

V. Вывод:

Коэффициент вязкости глицерина, определенный по методу Стокса равен:

h = (h_ср + Dh_ср ) = (... +...) Па ×с

Контрольные вопросы

1. Какие т-д системы называют неравновесными? Назовите основные явления переноса.

2. В чем заключается явление диффузии? Запишите закон Фика и поясните его суть.

3. В чем заключается явление теплопроводности? Запишите закон Фурье и поясните его суть.

4. В чем заключается явление вязкого трения? Запишите закон Ньютона и поясните его суть.

5. Как объясняются явления переноса с точки зрения молекулярно-кинетической теории?

6. Поясните, как явление внутреннего трения в жидкости иллюстрирует принцип противодействия Ле Шателье-Брауна.

7. Ламинарное и турбулентное течение жидкости. Критерий Рейнольдса.

8. Является ли определение вязкости по методу Стокса прямым или косвенным измерением?

9. Определите размерность коэффициента вязкости в системе Си, используя формулу Стокса.

10. Выведите расчетную формулу для коэффициента вязкости.

ЛАБОРАТОРНАЯ РАБОТА № 3 (I-I6)

Дата добавления: 2015-10-30