
|
Читайте также: |
При изучении той или иной генеральной совокупности нам неизвестен либо закон ее распределения, либо параметры распределения. В таких случаях в математической статистике выдвигается некоторое предположение относительно свойств генеральной совокупности. Такое предположение носит название статистической гипотезы.
Статистическая гипотеза может быть проверена на основании результатов случайной выборки.
Правило, устанавливающее условия, при которых проверяемая гипотеза принимается или отвергается, называется статистическим критерием.
Обработка экспериментальных данных с помощью любого критерия осуществляется по следующей схеме:
1. Берется один или два ряда наблюдений (одна или две выборки) и по элементам этих рядов по определенным формулам (для каждого критерия свои формулы) вычисляют статистики. Получают определенное число.
2. По заданному условию значимости 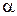 и числу степеней свободы
и числу степеней свободы 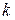 находят по таблицам (для каждого критерия свои таблицы), приводимым в приложении учебника по теории вероятностей и математической статистике, граничные значения для чисел, полученных в п.1. Если полученное в п.1 число не выходит за пределы найденных границ, то принимается следующее утверждение: нет достаточных оснований отвергнуть выдвинутую гипотезу.
находят по таблицам (для каждого критерия свои таблицы), приводимым в приложении учебника по теории вероятностей и математической статистике, граничные значения для чисел, полученных в п.1. Если полученное в п.1 число не выходит за пределы найденных границ, то принимается следующее утверждение: нет достаточных оснований отвергнуть выдвинутую гипотезу.
В математической статистике наиболее употребительными являются следующие критерии (или распределения): Стьюдента, Фишера (эти критерии исходят из предположения о нормальном законе распределения обследуемых признаков), 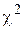 Пирсона, Колмогорова, Смирнова, Романовского, Ястремского и другие (эти критерии применяют для проверки наличия нормального и других распределений признака Х и когда не используются конкретные значения параметров этих распределений).
Пирсона, Колмогорова, Смирнова, Романовского, Ястремского и другие (эти критерии применяют для проверки наличия нормального и других распределений признака Х и когда не используются конкретные значения параметров этих распределений).
Критерий согласия Пирсона (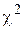 )
)
Критерий согласия Пирсона (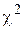 ) применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению при большом объеме выборки (
) применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению при большом объеме выборки (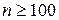 ) и больших частотах (
) и больших частотах (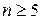 ) вариантов
) вариантов 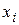 .
.
За меру расхождения эмпирического и теоретического распределений английский математик Пирсон принял величину 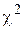 (хи квадрат)
(хи квадрат)
 , (26)
, (26)
где 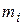 — эмпирические частоты,
— эмпирические частоты, 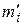 — теоретические частоты.
— теоретические частоты.
Применение критерия 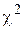 к проверке гипотезы о нормальном распределении генеральной совокупности значений признака Х осуществляется по следующему правилу.
к проверке гипотезы о нормальном распределении генеральной совокупности значений признака Х осуществляется по следующему правилу.
Правило применения критерия 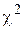 .
.
По имеющейся выборке сделать предположение о нормальном законе распределения признака Х генеральной совокупности. Затем найти оценки параметров этого закона, т.е. найти 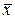 и
и 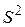 .
.
Вычислить теоретические частоты 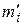 по формуле
по формуле
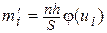 , (27)
, (27)
где n — объем выборки, h — шаг, S – выборочное среднее квадратическое отклонение, 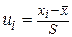 ,
, 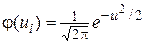 находится по таблице приложения №1.
находится по таблице приложения №1.
Для вычисления теоретических частот 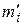 составить табл. 12.
составить табл. 12.
| Таблица 12 | ||||
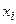
| 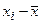
| 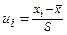
| 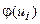
| 
|
Полученные частоты 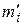 округлить до целых.
округлить до целых.
Вычислить величину 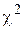 по формуле (26) и обозначить ее через
по формуле (26) и обозначить ее через 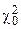 . Расчет вести, пользуясь табл. 13.
. Расчет вести, пользуясь табл. 13.
| Таблица 13 | ||||
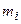
| 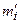
| 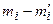
| 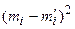
| 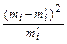
|
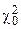
|
Найти число степеней свободы k (параметр распределения Пирсона) по формуле
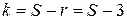 , (27)
, (27)
где S — число интервалов вариационного ряда, r — сумма числа параметров теоретического закона распределения. Для нормального распределения признака Х 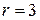 (учитываются параметры нормального распределения a и
(учитываются параметры нормального распределения a и  , а также объем выборки n).
, а также объем выборки n).
Выбрать уровень значимости 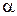 .
.
По найденному числу степеней свободы k и уровню значимости 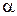 по таблице № распределения
по таблице № распределения 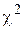 Пирсона определить критическое значение
Пирсона определить критическое значение 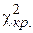 .
.
Если 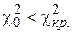 , то гипотеза о нормальном распределении признака Х принимается. Если
, то гипотеза о нормальном распределении признака Х принимается. Если 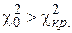 , то гипотеза о нормальном распределении признака Х отвергается.
, то гипотеза о нормальном распределении признака Х отвергается.
Критерий Пирсона можно применять для проверки гипотезы о том, что данная выборка взята из генеральной совокупности, распределенной по биномиальному закону, по закону Пуассона, по экспоненциальному закону.
Рассмотрим гипотезу 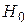 о распределении генеральной совокупности по закону Пуассона:
о распределении генеральной совокупности по закону Пуассона:
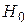 :
: 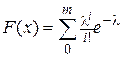 , (28)
, (28)
где 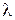 — параметр распределения Пуассона. Для применения критерия
— параметр распределения Пуассона. Для применения критерия 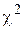 надо рассчитать теоретические частоты
надо рассчитать теоретические частоты 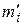 , а также получить по значениям выборки оценку параметра
, а также получить по значениям выборки оценку параметра 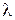 . Методом максимального правдоподобия доказывается, что выборочная средняя
. Методом максимального правдоподобия доказывается, что выборочная средняя 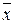 является пригодной оценкой для
является пригодной оценкой для 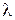 , то есть
, то есть 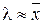 . Теоретические частоты
. Теоретические частоты 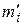 вычисляются по формуле
вычисляются по формуле
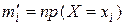 (29)
(29)
Вероятности 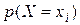 вычисляются по формуле
вычисляются по формуле
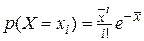 (30)
(30)
Так как при расчете теоретических частот 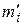 используется один параметр
используется один параметр 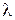 , то число степеней свободы k находят по формуле
, то число степеней свободы k находят по формуле
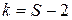 (31)
(31)
Затем вычисляют величину 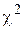 по формуле 26, обозначают ее через
по формуле 26, обозначают ее через 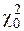 .По заданному уровню значимости
.По заданному уровню значимости 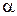 и найденному числу степеней свободы
и найденному числу степеней свободы 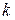 по таблице распределения
по таблице распределения 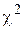 Пирсона находят
Пирсона находят 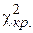 . Если
. Если 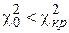 , то гипотеза
, то гипотеза 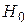 принимается, то есть делаем вывод, что признак Х распределен по закону Пуассона. Если
принимается, то есть делаем вывод, что признак Х распределен по закону Пуассона. Если 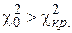 , то гипотеза
, то гипотеза 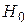 отвергается.
отвергается.
Критерий Романовского.
Для оценки близости эмпирического распределения признака Х к нормальному теоретическому Романовский предложил вычислять отношение:
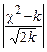 , (32)
, (32)
где 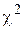 — статистика критерия Пирсона, вычисленная по формуле (26), используя опытные данные, k — число степеней свободы, найденное по формуле (27). Если указанное отношение по модулю меньше трех, то расхождение между теоретическим и эмпирическим распределениями считается несущественным, то есть можно принять за закон данного эмпирического распределения нормальное распределение. Если отношение (32) больше трех, то делаем вывод о том, что эмпирическое распределение признака Х не подчиняется нормальному закону распределения.
— статистика критерия Пирсона, вычисленная по формуле (26), используя опытные данные, k — число степеней свободы, найденное по формуле (27). Если указанное отношение по модулю меньше трех, то расхождение между теоретическим и эмпирическим распределениями считается несущественным, то есть можно принять за закон данного эмпирического распределения нормальное распределение. Если отношение (32) больше трех, то делаем вывод о том, что эмпирическое распределение признака Х не подчиняется нормальному закону распределения.
Критерий Колмогорова.
Критерий Колмогорова в своем классическом виде является более мощным, чем критерий Пирсона и может быть использован для проверки гипотезы о соответствии эмпирического распределения любому теоретическому непрерывному распределению 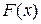 с заранее известными параметрами. Однако параметры функции распределения
с заранее известными параметрами. Однако параметры функции распределения 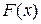 , как правило, нам неизвестны и их оценка производится по данным самой выборки. Это обстоятельство накладывает ограничения на возможность широкого практического применения критерия, а может быть использовано только для проверки соответствия опытных данных лишь некоторым конкретным функциям распределения.
, как правило, нам неизвестны и их оценка производится по данным самой выборки. Это обстоятельство накладывает ограничения на возможность широкого практического применения критерия, а может быть использовано только для проверки соответствия опытных данных лишь некоторым конкретным функциям распределения.
Для проверки соответствия эмпирического распределения теоретическому нормальному распределению критерий Колмогорова применяют следующим образом
Вычисляется статистика критерия Колмогорова 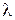 по формуле
по формуле
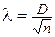 , (33)
, (33)
где 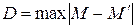 — максимум абсолютного значения разности между накопленными эмпирическими частотами М и накопленными теоретическими частотами
— максимум абсолютного значения разности между накопленными эмпирическими частотами М и накопленными теоретическими частотами 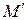 , n — объем выборки.
, n — объем выборки.
По вычисленному 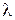 находят вероятность
находят вероятность 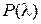 — вероятность того, что
— вероятность того, что 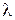 достигает данной величины. Вероятность
достигает данной величины. Вероятность 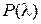 находят, пользуясь табл. 14.
находят, пользуясь табл. 14.
| Таблица 14 | |||
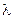
| 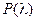
| 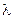
| 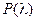
|
| 0,30 | 1,0000 | 1,10 | 0,1777 |
| 0,35 | 0,9997 | 1,20 | |
| 0,40 | 1,30 | ||
| 0,45 | 1,40 | 0,397 | |
| 0,50 | 1,50 | 0,222 | |
| 0,55 | 1,60 | 0,120 | |
| 0,60 | 1,70 | 0,052 | |
| 0,70 | 1,90 | 0,015 | |
| 0,75 | 2,00 | ||
| 0,80 | 2,10 | ||
| 0,85 | 2,20 | ||
| 0,90 | 2,30 | ||
| 0,95 | 2,40 | ||
| 1,00 | 2,50 |
Если найденному значению 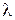 соответствует очень малая вероятность, то есть
соответствует очень малая вероятность, то есть 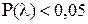 , то расхождение между эмпирическим и теоретическим распределениями нельзя считать случайным. Следовательно, рассматриваемая выборка не подчиняется нормальному закону распределения. Если вероятность
, то расхождение между эмпирическим и теоретическим распределениями нельзя считать случайным. Следовательно, рассматриваемая выборка не подчиняется нормальному закону распределения. Если вероятность 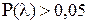 , то расхождение между частотами может быть случайным и распределения хорошо соответствуют одно другому.
, то расхождение между частотами может быть случайным и распределения хорошо соответствуют одно другому.
Если проверяют гипотезу по критерию Колмогорова о соответствии выборки экспоненциальному распределению, параметры которого оценивают по опытным данным, то сначала вычисляют статистики [ ]
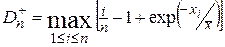 (34)
(34)
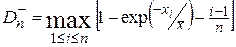 (35)
(35)
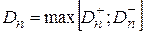 (36)
(36)
Затем составляют неравенство
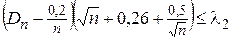 (37)
(37)
Критические значения 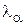 для этого случая:
для этого случая: 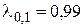 ,
, 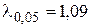 и
и 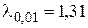 . Если неравенство (37) при выбранном
. Если неравенство (37) при выбранном 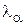 выполняется, то это означает, что опытные данные не противоречат предположению о соответствии их экспоненциальному распределению.
выполняется, то это означает, что опытные данные не противоречат предположению о соответствии их экспоненциальному распределению.
Критерий Б.С. Ястремского.
Для проверки соответствия данной нормальному распределению составляется неравенство
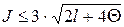 , (38)
, (38)
где
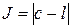 ;
;
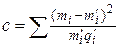 ;
;
 — эмпирические частоты;
— эмпирические частоты;
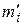 — теоретические частоты;
— теоретические частоты;
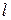 — число вариантов дискретного вариационного ряда;
— число вариантов дискретного вариационного ряда;
 ;
; 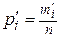 ; n — объем выборки. Если
; n — объем выборки. Если 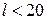 , то
, то 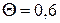 .
.
Если вычисленное значение 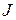 меньше
меньше 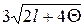 , то за закон эмпирического распределения признака Х можно принять теоретический закон нормального распределения. При значениях
, то за закон эмпирического распределения признака Х можно принять теоретический закон нормального распределения. При значениях 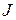 больших
больших 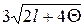 расхождения между эмпирическим и теоретическим распределениями существенно. В этом случае данные выборки не будут подчиняться нормальному закону распределения.
расхождения между эмпирическим и теоретическим распределениями существенно. В этом случае данные выборки не будут подчиняться нормальному закону распределения.
Для вычисления величины 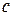 составляется табл. 15.
составляется табл. 15.
| Таблица 15 | ||||||||
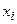
| 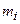
| 
| 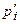
| 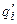
| 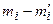
| 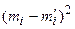
| 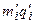
| 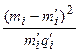
|
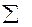
| 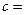
|
Приближенные критерии нормальности распределения.
Для приближенной проверки гипотезы о нормальном распределении выборочной совокупности используют выборочные статистики: асимметрию и эксцесс. В этом случае названные статистики вычисляют по формулам (18) и (19). Затем вычисляют их средние квадратические отклонения по формулам
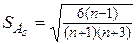 (39)
(39)
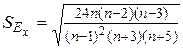 (40)
(40)
Если 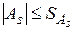 и
и 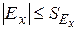 , то выборочная совокупность подчиняется нормальному закону распределения. Если
, то выборочная совокупность подчиняется нормальному закону распределения. Если 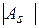 и
и 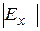 заметно больше своих средних квадратических отклонений, то выборочная совокупность не будет распределена по нормальному закону.
заметно больше своих средних квадратических отклонений, то выборочная совокупность не будет распределена по нормальному закону.
Проверку выборочной совокупности на нормальное распределение можно производить, используя статистики 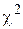 ,
,  и
и 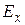 . Сначала вычисляют статистику
. Сначала вычисляют статистику 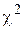 по формуле
по формуле
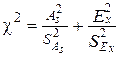 (41)
(41)
Затем при заданном уровне значимости 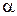 и числе степеней свободы
и числе степеней свободы 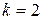 (используют в расчетах две статистики
(используют в расчетах две статистики  и
и 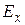 ) по табл. № приложения для распределения
) по табл. № приложения для распределения 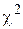 Пирсона находят
Пирсона находят 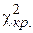 . Если выполняется неравенство
. Если выполняется неравенство 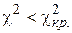 , то гипотезу о нормальном распределении выборочной совокупности принимают. В противном случае, то есть когда
, то гипотезу о нормальном распределении выборочной совокупности принимают. В противном случае, то есть когда 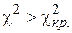 , гипотезу о нормальном распределении выборки отвергают.
, гипотезу о нормальном распределении выборки отвергают.
Покажем применение рассмотренной теории на примере выполнения лабораторной работы №2, являющейся продолжением лабораторной работы №1.
Контрольные вопросы.
Рассказать о возможных вариантах построения кривой нормального распределения по опытным данным.
Дать определение статистической гипотезы.
Что называется статистическим критерием?
Сформулировать алгоритм применения любого статистического критерия для обработки экспериментальных данных.
Сформулировать правило применения критерия согласия Пирсона (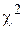 ) для проверки гипотезы согласованности эмпирического распределения с теоретическим нормальным.
) для проверки гипотезы согласованности эмпирического распределения с теоретическим нормальным.
Рассказать о применении критерия согласия Романовского для оценки близости эмпирического распределения к теоретическому нормальному.
Сформулировать алгоритм применения критерия Колмогорова для проверки соответствия эмпирического распределения нормальному теоретическому распределению.
Рассказать о применении критерия Б.С. Ястремского для проверки соответствия данной выборочной совокупности нормальному распределению.
Рассказать о приближенных критериях, применяемых для проверки гипотезы о нормальном распределении выборочной совокупности.
Лабораторная работа №2
Построение кривой нормального распределения по опытным
данным. Проверка гипотезы о нормальном распределении выборки.
Цель работы: овладение студентом способами построения эмпирической и теоретической (нормальной) кривой распределения; выработка умения и навыков применения критериев согласия для проверки выдвинутой статистической гипотезы.
Содержание работы: на основе дискретного вариационного ряда, полученного в лабораторной работе №1, выполнить следующее:
Построить эмпирическую (полигон) и теоретическую (нормальную) кривую распределения.
Проверить согласованность эмпирического распределения с теоретическим нормальным, применяя три критерия:
а) критерий Пирсона;
б) один из критериев: Колмагорова, Романовского или Ястремского;
в) приближенный критерий.
Методика выполнения работы.
Продолжим вероятностно-статистическую обработку результатов эксперимента, предложенных в лабораторной работе №1, то есть обводненности нефти из насосных скважин. За основу берем дискретный вариационный ряд (табл. 8):
варианты, 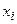
| 60,15 | 60,45 | 60,75 | 61,05 | 61,35 | 61,65 | 61,95 | 62,25 | 62,55 | 62,85 |
частоты, 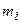
|
а так же значения 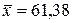 и
и 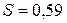 .
.
Эмпирическая кривая распределения представляет собой полигон частот (смотри лабораторную работу №1). Для построения теоретической (нормальной) кривой найдем координаты точек 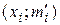 , для чего рассчитаем теоретические частоты
, для чего рассчитаем теоретические частоты 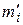 (табл. 16).
(табл. 16).
| Таблица 16. | ||||||
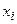
| 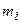
| 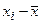
| 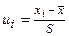
| 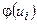
|  
| 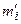
|
| 60,15 | -1,23 | -2,08 | 0,0459 | 2,3 | ||
| 60,45 | -0,93 | -1,58 | 0,1145 | 5,8 | ||
| 60,75 | -0,63 | -1,07 | 0,2251 | 11,4 | ||
| 61,05 | -0,33 | -0,56 | 0,3410 | 17,3 | ||
| 61,35 | -0,03 | -0,05 | 0,3984 | 20,3 | ||
| 61,65 | 0,27 | 0,46 | 0,3589 | 18,2 | ||
| 61,95 | 0,57 | 0,97 | 0,2492 | 12,7 | ||
| 62,25 | 0,87 | 1,47 | 0,1354 | 6,9 | ||
| 62,55 | 1,17 | 1,98 | 0,0562 | 2,9 | ||
| 62,85 | 1,47 | 2,49 | 0,0180 | 0,9 |
Строим эмпирическую и теоретическую кривые (рис. 5).

Проверим согласованность эмпирического распределения (обводненности нефти из насосных скважин) с теоретическим нормальным по критерию Пирсона. Вычислим величину 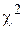 по формуле (26):
по формуле (26):
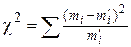 .
.
Для нахождения суммы составляем расчетную табл. 17.
| Таблица 17 | ||||
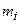
| 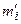
| 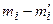
| 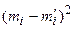
| 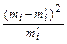
|
| 0,5 | ||||
| -2 | 0,363636 | |||
| 0,058824 | ||||
| 4,05 | ||||
| -2 | 0,222222 | |||
| -11 | 9,307692 | |||
| 2,285714 | ||||
| 1,333333 | ||||
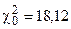
|
Находим число степеней свободы 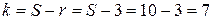 . Выбираем уровень значимости
. Выбираем уровень значимости 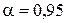 . По таблице критических точек распределения
. По таблице критических точек распределения 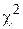 (приложение) находим
(приложение) находим 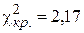 . Так как
. Так как 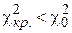
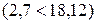 , то делаем вывод, что данные выборки, характеризующие обводненность нефти из насосных скважин не подчиняются нормальному закону распределения.
, то делаем вывод, что данные выборки, характеризующие обводненность нефти из насосных скважин не подчиняются нормальному закону распределения.
Проведём проверку близости эмпирического распределения k нормальному по критерию Романовского. Вычислим величину
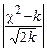 .
.
У нас,  ,
, 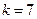 . Тогда
. Тогда 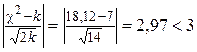 , то есть расхождение между эмпирическим и теоретическим распределением несущественно, что позволяет утверждать, что данные выборки, характеризующие обводненность нефти из насосных скважин по критерию Романовского подчиняются нормальному закону распределения. К такому же выводу мы приходим, применяя критерий Колмогорова (проверить самостоятельно).
, то есть расхождение между эмпирическим и теоретическим распределением несущественно, что позволяет утверждать, что данные выборки, характеризующие обводненность нефти из насосных скважин по критерию Романовского подчиняются нормальному закону распределения. К такому же выводу мы приходим, применяя критерий Колмогорова (проверить самостоятельно).
И, наконец, проведём проверку близости рассматриваемой выборки к нормальному распределению по приближенному критерию, используя выборочные статистики асимметрию, эксцесс и их средние квадратические отклонения. В лабораторной работе №1 были найдены 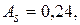
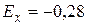 . Средние квадратические отклонения для асимметрии и эксцесса находим по формуле (39) и (40):
. Средние квадратические отклонения для асимметрии и эксцесса находим по формуле (39) и (40):
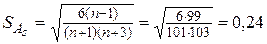
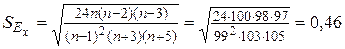
Так как 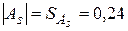 и
и 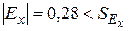 , то делаем вывод, что данные выборки, характеризующие обводненность нефти из насосных скважин подчиняются нормальному закону распределения.
, то делаем вывод, что данные выборки, характеризующие обводненность нефти из насосных скважин подчиняются нормальному закону распределения.
Итак, для проверки согласованности эмпирического распределения с теоретическим нормальным применили 4 критерия, три из них подтвердили близость выборочной совокупности к нормальному распределению. Поэтому окончательно заключаем, что за закон распределения признака Х — обводненности нефти из насосных скважин можно принять нормальное распределение.
Замечание.
В качестве вариантов заданий для выполнения лабораторной работы №2 следует брать дискретные вариационные ряды из лабораторной работы №1, а так же значения статистик 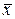 ,
, 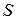 ,
, 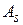 ,
, 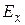 .
.
Дата добавления: 2015-10-29; просмотров: 281 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Распределения | | | Задачи теории корреляции |