Составление вариационных рядов.

Группа чисел, объединяемая каким-либо признаком, называется совокупностью.

Задача заключается в том, чтобы составить вариационный ряд из данной совокупности и воспользоваться его показателями для получения требуемой информации.

Пример. У 34 спортсменов-лыжников зарегистрировано такое время восстановления пульса после прохождения дистанции (в секундах):

81; 78: 84; 90; 78; 74; 84; 85; 81; 84: 79; 84; 74; 84; 84; 84; 84;

85; 81; 84; 78: 81; 74; 84; 81; 84; 85; 81; 78; 81; 81; 84; 78; 81.

После ранжирования вариационный ряд данной совокупности чисел представляется следующим образом:

Таблица1.1.

хi	ni
	n=34

Числа, представляющие собой результаты измерений (х_i), называют вариантами; n _i — числа их повторений — называются частотами; n — сумма всех частот — есть объем совокупности.

Полученный вариационный ряд, можно представить графически. Для построения графика, необходимо, прежде всего, условиться о масштабе на горизонтальной и вертикальной оси.

В данной задаче на горизонтальной оси будем откладывать значения времени восстановления пульса (х_i) таким образом, что единице длины, избранной произвольно, соответствует значение одной секунды. На вертикальной оси отложим значения частот нашего ряда (n _i), принимая масштаб: единица длины равна единице частоты.

Рис. 1. Графическое представление вариационного ряда.

На рис. 1 видно:

1) из всех обследованных наибольшую группу составили спортсмены, время восстановления пульса у которых 84 с;

2) у многих это время 81 с;

3) наименьшую группу составили спортсмены с малым временем восстановления пульса — 74 с и большим — 90 с.

2. Параметры вариационных рядов.

Основными характеристиками вариационных рядов являются: средняя арифметическая, среднее линейное отклонение, дисперсия, среднее квадратическое, отклонение, коэффициент вариации, мода и медиана. Рассмотрим способы их вычисления.

2.1. Мода.

Мода (Mo) — это такое значение в множестве наблюдений, которое встречается наиболее часто. В совокупности значений (2, 6, 6, 8, 7, 3,3, 9, 9, 9, 10) модой является 9, потому что оно встречается чаще любого другого значения. В случае, когда все значения в группе встречаются одинаково часто, считают, что эта группа не имеет моды.

Когда два соседних значения имеют одинаковую частоту и они больше частоты любого другого значения, мода есть среднее этих двух значений (10, 11, 11, 11, 12,12,12, 13, 14, 14, 17 – мода 11,5).

Если два значения, не являющиеся соседними, имеют равные частоты, и они больше частот любого значения, то существуют две моды (10, 11, 11, 11, 12, 13, 14, 14, 14, 17- моды 11 и 14); в таком случае группа измерений или оценок является бимодальной. Наибольшей модой в группе называется единственное значение, которое удовлетворяет определению моды. Однако во всей группе может быть несколько меньших мод. Эти меньшие моды представляют собой локальные вершины распределения частот. В таблице 1.1 модой является Mo =84, т.к. данной варианте соответствует наибольшая частота (n _i=11).

2.2. Медиана.

Медиана (Me) — это значение, которое делит упорядоченное множество данных пополам, так что одна половина значений оказывается больше медианы, а другая — меньше. Для нахождения медианы вводится понятие накопленных частот (m_i). Рассмотрим это на примере Таблицы 1.1.

Под накопленными частотами подразумеваются суммы частот, получаемые от последовательного сложения. Так, для спортсменов, показавших время восстановления пульса, не превышающее значение первого варианта 74 с, было 4; не превышающее 78 с, было 10 (4 показали 74 с и 6—78 с), не превышающее 81 с — 19 человек и т.д. Последняя накопленная частота должна соответствовать, естественно, объему совокупности.

Пример 2.2.1.

xi	ni	mi
	n=34

Общее количество объектов, рассматриваемых в данном примере, было n=34. Объекты, стоящие посередине ряда, будут по номеру 17-й и 18-й. По накопленным частотам определяем варианты, соответствующие 17-му и 18-му объектам. В данном случае как 17-й, так и 18-й объекты находятся в третьей строке, так как накопленная частота 19 содержит в себе 17-й и 18-й объекты. Ей соответствующий вариант 81 с и есть медиана.

Если окажется, что один из объектов, стоящих посередине ряда, принадлежит одной строке, а другой — следующей строке, медиана определяется как средняя арифметическая между обоими вариантами.

В случае если объем совокупности представляет собой нечетное число, вариант, стоящий посередине ряда, будет один. Например, при n=17 таким вариантом должен быть 9-й объект, при n=23 — 11-й и т. д. В этом случае медиана определяется так же, как и в случае четного объема совокупности.

2.3. Среднее арифметическое.

Пусть имеется n объектов, у которых измеряем некоторую характеристику, и получаем значения х₁ х₂,..., х_n. Самым характерным и существенным параметром вариационного ряда является средняя арифметическая величина. Она показывает средний уровень всех измерений для данной группы чисел и вычисляется следующим образом:

1. Каждый вариант (х_i) надо умножить на свою частоту (n_i), т. е – (х_in_i).

2. Полученные произведения (х_in_i) необходимо сложить от первого до последнего показания, т. е.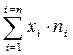

3. Найденную сумму 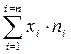следует разделить на объем совокупности, т. е. -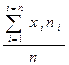

Обозначим среднюю арифметическую как Х. Тогда формула взвешенной средней выглядит так:

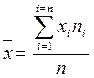
где Σ - знак суммирования; n – объем совокупности (количество объектов).

Для примера 2.2.1 среднее арифметическое вычисляется следующим образом:

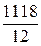= = 93,1 ≈93

Мода наиболее просто вычисляется — ее можно определить на глаз. Более того, для очень больших групп данных это достаточно стабильная мера центра распределения.

Медиана занимает промежуточное положение между модой и средним с точки зрения ее вычисления. Эта мера получается особенно легко в случае ранжированных данных.

Среднее множество данных предполагает в основном арифметические операции. На величину среднего влияют значения всех результатов. Медиана и мода не требуют для определения всех значений. Посмотрим, что произойдет со средним, медианой и модой, когда удвоится максимальное значение в следующем множестве: (1,3,3,5,6,7,8)

Множество		Me	Mo
1,3,3,5,6,7,8	33/7
1,3,3,5,6,7, 16	41/7

На величину среднего особенно влияют данные, находящиеся далеко от центра группы оценок.

2.4. Среднее квадратическое отклонение ().Дисперсия ( ²).

В практике статистических исследований в качестве меры рассеивания очень часто используется среднее квадратическое, или стандартное, отклонение . Его квадрат ( ²) называется дисперсией. Эмпирическая дисперсия ряда измерений объема n определяется по формуле:

Соответственно, среднее квадратическое отклонение:

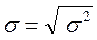
Среднее квадратическое отклонение — величина именованная и выражается в тех же единицах измерения, что и признак. Чем сильнее варьирует признак, тем больше и величина среднего квадратического отклонения, и, наоборот, при слабом варьировании признака среднее квадратическое отклонение будет меньше.

Значения ² и для примера 2.2.1:

=

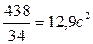
σ = 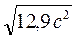=3,6с.

Средняя арифметическая и среднее квадратическое отклонение дают полную количественную характеристику любой эмпирической совокупности. Среднее арифметическое отражает действие на признак основных причин, определяющих типичный для множества уровень его развития, тогда как среднее квадратическое отклонение характеризует варьирование значений этого признака вокруг центра распределения, т.е. средней арифметической. Среднее квадратическое отклонение является мерой степени влияния на признак различных второстепенных причин, вызывающих его варьирование.

2.5. Коэффициент вариации.

Среднее квадратическое отклонение является основным мерилом вариабельности признаков. Этот показатель не зависит от числа наблюдений, и поэтому может использоваться для сравнительной оценки варьирования однородных признаков. Вместе с тем среднее крадратическое является величиной именованной, и поэтому не может быть использована для сравнения варьирования признаков, выраженных разными единицами измерения.

Чтобы среднее квадратическое отклонение могло быть использовано в качестве меры сравнения вариабельности признаков независимо от того, какими единицами измерения они выражены, его принято выражать в процентах от средней арифметической. Полученный таким образом показатель является числом относительным, выражающим изменчивость признака в процентах, его называют коэффициентом вариации:

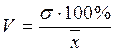
Величина коэффициента вариации определяется отношением абсолютных значений двух основных характеристик вариационного ряда – средней арифметической и среднего квадратического отклонения. При нормальном распределении коэффициент вариации не превышает 10 – 15%. В спортивных исследованиях применение интервала 10 – 15% для определения однородности объектов является весьма условным. Здесь само понятие «однородность» или «неоднородность» объектов содержит различный смысл в зависимости от того, какие объекты исследуются.

Для примера 2.2.1 коэффициент вариации вычисляется следующим образом:

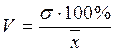=4,5%.

Элементы комбинаторика Основные понятия теории вероятностей. Нормальный закон распределения.

Дата добавления: 2015-10-24