Достоверность различия между двумя выборочными средними.

Рассмотрим задачу сравнения средних арифметических двух генеральных совокупностей посредством сравнения выборочных средних. Разность средних называется недостоверной, т. е. случайной, в том случае, если она несущественна и объясняется случайными причинами. Достоверной, т. е. неслучайной, она бывает тогда, когда различие средних существенно и объяснимо влиянием определенных факторов.

Прежде чем перейти к описанию метода, остановимся на вопросе о том, где в спорте складывается аналогичная приведенной ситуация. Данная ситуация возникает тогда, когда необходимо сравнивать между собой какие-либо группы чисел.

Это могут быть, например, показатели спортсменов в определенной специализации до и после серии тренировок для выявления сдвигов в этих показателях – доказательства эффективности тренировочного процесса и т. д. В этом случае наличие существенного различия между параметрами совокупностей укажет на принципиальное отличие по рассматриваемому признаку.

Для определения достоверности различия между двумя выборочными средними необходимо предварительно обработать числа обеих сравниваемых групп по способу вариационных рядов, т. е. определить в обеих группах средние арифметические и средние квадратические отклонения s.

Критерием определения достоверности различия является величина, определяемая по формуле:

(4.3.1)

t – критерий достоверности различия разности выборочных средних;

х₁ – средняя арифметическая первой группы чисел;

х_{2 –} средняя арифметическая второй группы чисел;

| x₁ – х₂ | — разность между средними, рассматриваемая без учета знака (т. е. всегда со знаком плюс, каким бы ни был этот знак в действительности);

m₁ – ошибка репрезентативности первой группы чисел;

m₂ – ошибка репрезентативности второй группы чисел.

Определенный по формуле (4.3.1) критерий подлежит сравнению с некоторым граничным значением t_гр.

Граничный критерий находится по специальной таблице Стьюдента для заданной надежности и объема выборок (см. приложение 2).

Если в результате сравнения t, найденного по формуле (4.3.1), и t_гр, окажется, что t ≥ t_гр. (больше или равно t_гр.), разность между сравниваемыми выборочными показателями называется достоверной.

Если при сравнении окажется, что t < t _гр, (меньше t _гр.), разность между выборочными показателями называется недостоверной, существенность в различии не доказана. В этом случае можно предположить не только несущественность различия между совокупностями, но и неправильный подбор выборки, в частности недостаточную ее численность.

В последнем случае следует пересмотреть состав выборочных совокупностей и повторить еще раз всю последовательность действий.

Рассмотренный метод называется критерий Стьюдента, используется для исследования равновеликих выборок. Соответствие нормальному закону распределению обязательно. Критерий применяется в случае сравнения выборок по абсолютным значениям их средних арифметических. В практике спорта пригоден для сравнения групп по значению их средних показателей.

Пример 4.3.1. Из контрольной и экспериментальной групп боксеров выбрано по 12 человек, у которых измерено время простой реакции на один и тот же раздражитель. Полученные измерения: х _i—время реакции боксера (в мс), n _i—количество спортсменов, показавших данное время, приведены ниже и обработаны в форме таблицы методом средних величин. Контрольная группа (табл. 4.3.1):

Таблица 4. 3.1

xi	ni	xini	xi-	(xi- )^2	(xi- )^2ni
			-18
			-8
			+2
			+12
			+22
	n =12

Экспериментальная группа (табл. 4.3.2):

Таблица 4.3.2

xi	ni	xini	xi-	(xi- )^2	(xi- )^2ni
			-18
			-8
			+2
			+12
			+22
	n =12

Для того, чтобы выяснить имеется ли сдвиг в показаниях данных спортсменов и существенен ли он, надо вначале сравнить их средние показания. В контрольной группе ₁ = 568 мс и в экспериментальной группе ₂ = 568 мс. Это говорит о том, что средние показатели экспериментальной группы не изменились в сравнении с контрольной и ожидаемого сдвига вообще не произошло. В таком случае критерий достоверности должен указать на несущественность сдвига в средних показателях, т. е. мы должны получить недостоверность выборочных средних. Для того чтобы в этом убедиться, проведем расчет.

По формуле (4.2.2) найдем ошибки репрезентативности для контрольной и экспериментальной групп:

для контрольной –

для экспериментальной –

Находим критерий достоверности по формуле (4.3.1):

Как видим из вычислений, минимальный критерий t = 0 получился за счет равенства двух средних арифметических. Далее обращаемся к таблице Стьюдента и, задавшись надежностью P₁ =0,95 (что равноценно уровню значимости b₁=0,05), находим граничный критерий t _гр. = 2,20.

Таким образом, t, полученное по формуле при расчете наших групп, есть t = 0, а граничное t _гр. = 2,20. Следовательно, t < t _гр. (т. е. критерий меньше граничного) и разность выборочных средних недостоверна.

В этом случае возникает неопределенность: либо недостоверность средних указывает на несущественность сдвига средних и новая методика, апробированная данной экспериментальной группой, неэффективна, либо выборочная совокупность была нерепрезентативной, например, вследствие своей малочисленности. Для того чтобы проверить последнее обстоятельство, возвратимся к первоначальным измерениям, однако подберем выборочные совокупности более объемные. При этом оставим, конечно, неизменным и сам эксперимент, и технику его исполнения, и точность измерений.

Ниже приводим снова две таблицы для контрольной (4.3.3) и экспериментальной (4.3.4) групп. В каждой группе по 40 спортсменов. Их результаты также обработаны методом средних величин.

Таблица 4.3.3

x i	ni	xini	xi-	(xi- )^2	(xi- )^2ni
			—38 —28 —18 —8 +2 +12 +22
	n =40

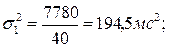
Таблица 4.3.4

xi	ni	xini	xi-	(xi- )^2	(xi- )^2ni
			-18 —8 +2 +12 +22 +32 +42
	n =40

Как видим из расчетов, при малочисленных выборках n = 12 контрольная группа показала в среднем ₁ = 568 мс, а экспериментальная ₂ = 568 мс. При увеличении объема выборочной совокупности до n = 40 эти числа оказались ₁ = 588 мс, ₂ = 568 мс. Значит, экспериментальная группа хорошо была представлена 12 спортсменами и показала в обоих случаях стабильную величину средней реакции ₂ = 568 мс. Контрольная же группа показала при увеличении объема выборки другой результат ₁ = 588 мс, следовательно, ее малочисленная выборка n = 12 плохо репрезентатировала генеральную.

Теперь среднее значение времени реакции у боксеров экспериментальной группы ₂ = 568 мс ниже, чем время реакции спортсменов контрольной группы ₁ = 588 мс, различие между ними существует и теперь есть смысл выявить существенность этого сдвига.

По формуле (4.2.1) вычисляем ошибки репрезентативности для обеих групп:

для контрольной –

для экспериментальной –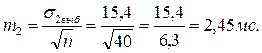

Находим критерий достоверности по формуле (3.3.1):

Обращаемся к таблице Стьюдента и находим, что при заданной надежности P₁ = 0,95 (уровень значимости b₁=0,05) и при n=40, t _гр. = 2,02.

Таким образом, найденный критерий t = 6,06 больше граничного t _гр . = 2,02 (t > t _гp.) и разность выборочных средних достоверна – сдвиг в значениях средних величин существенен, объясняется закономерными, неслучайными обстоятельствами и может быть указателем, что новая методика дает ощутимые изменения.

Из приведенного примера ясно, что в случае установленной достоверности выборочных средних можно сделать вывод о существенности и закономерности сдвига в средних величинах. В случае недостоверности, такого вывода сделать нельзя и возникает две необходимости: либо продолжать исследования при измененной и улучшенной с точки зрения репрезентативности выборочной совокупности, либо не пользоваться данным методом вообще. Количество повторений в изменении выборок зависит от условий эксперимента и диктуется, как правило, возможностью увеличения объема выборочной совокупности.

Мы сравнивали средние арифметические выборок, но можно сравнивать и другие характеристики выборок. Для этого существуют свои методы. Рассмотрим некоторые из них.

Критерий Фишера. Применяется для сравнения разновеликих малых и средних выборок. Соблюдение нормального закона распределения необязательно. Сравниваются средние квадратические отклонения s выборок. Таким образом, критерий применяется в случае сравнения групп по фактору рассеивания, т.е. оценивается сравнительная характеристика на стабильность.

Определяется критерий Фишера по формуле

(4.3.2)

где , - средние квадратические отклонения сравниваемых выборок. При этом >

При заданной надежности Р и объемах сравниваемых выборок n₁ и n₂ из таблицы Фишера находим граничное значение критерия F _гр. При сравнении критериев определяем достоверность различия: если F ≥ F_гр – достоверно; если F < F_гр – недостоверно.

Пример 4.3.2. Поглощение кислорода, л/мин, измерено во время длительной работы на выносливость у двух групп спортсменов х_i и y_i. Определить принципиально ли отличие между этими группами по стабильности поглощения кислорода.

Таблица 4. 3.5

xi	ni	xini	xi-	(xi- )^2	(xi- )^2ni
4,0 4,1 4,2 4,4 4,6 4,7		28,0 36,9 33,6 44,0 18,4 14,1	- 0,3 - 0,2 - 0,1 +0,1 +0,3 +0,4	0,09 0,04 0,01 0,01 0,09 0,16	0,63 0,36 0,08 0,10 0,36 0,48
	n1 = 41	175,0			2,01

Таблица 4. 3.6

уi	ni	уini	уi-	(уi- )^2	(уi- )^2ni
4,0 4,3 4,5 4,6 4,7		8,0 17,2 40,5 13,8 4,7	-0,4 -0,1 +0,1 +0,2 +0,3	0,16 0,01 0,01 0,04 0,09	0,32 0,04 0,09 0,12 0,09
	n2 = 19	84,2			0,66

Находим критерий Фишера по формуле (4.3.2):

При надежности Р = 0,95, объемах выборок n₁ = 41 и n₂ = 19 граничное значение критерия по таблице Фишера F_гр = 2,0. Поскольку 1,4 < 2,0 (F < F_гр) различие между группами статистически недостоверно, т.е. группы различимы несущественно.

Рассмотренные критерии являются параметрическими, т.е. требуют расчета числовых характеристик выборок. Существуют критерии непараметрические в которых не требуется расчета числовых характеристик выборок.

Критерий Вилкоксона применяется как непараметрический для сравнения больших равновеликих выборок. Соответствие нормальному закону распределения необязательно. Критерий применим в случае попарного сравнения групп. Рассмотрим на примере.

Пример 4.3.3. Сравнить две группы пловцов х_i и у_i по показателю эффективности дыхания. Установить, достоверно ли различимы эти группы по эффективности дыхания.

Как видно из таблицы 4.3.7 каждой паре исходных данных соответствует разность х_i – у_i. Этой разности назначается ранг, т.е. определяется ее порядковый номер. При этом не учитывается знак разности и равным разностям назначаются равные ранги (среднее между номерами), а нулевая разность исключается из рассмотрения.

Таблица 4. 3.7

хi	уi	хi - уi	W	W(+)	W(-)
0.41 0.46 0.44 0.49 0.49 0.50 0.60 0.61 0.60 0.64	0,45 0,42 0,48 0,46 0,52 0,50 0,55 0,57 0,63 0,62	–0,04 +0,14 –0,14 +0,03 –0,03 +0,05 +0,04 –0,03 +0,05	–	– – – – –	– – – – – –

Ранги, относящиеся к положительным разностям выписываются в столбец W(+), относящиеся к отрицательным – в столбец W(–). Ранги в столбцах W(+) и W(–) суммируем. Меньшая из этих сумм – критерий Вилкоксона W.

Как видно из таблицы критерий Вилкоксона W =20.

Для надежности Р = 0,95 при n = 9 (т.е. 10 – 1), из таблицы Вилкоксона находим граничное значение критерия W_гр = 7.

Достоверность различия определяется из неравенства W ≥ W_гр – недостоверно; W < W_гр – достоверно.

В примере при Р = 0,95, n = 9, W_гр = 7, W = 20.

Поскольку W ≥ W_гр, различие между сравниваемыми выборками недостоверно. Требуется дополнительный анализ.

Критерий Уайта применяется как непараметрический для сравнения больших разновеликих выборок. Соблюдение нормального закона распределения необязательно.

Для определения критерия Уайта ранжируем исходные данные по двум линиям, соответствующим сравниваемым группам. Рассмотрим пример.

Пример 4.3.4. У спортсменов 16 лет измерена становая сила, Н, в группе баскетболистов х_i и футболистов у_i. Оценить, принципиально ли отличие этих группы по становой силе.

Таблица4.3.8		Таблица4.3.9
хi	ni		yi	ni
9,82 9,90 10,01 10,24 10,50 10,82			9,50 9,56 9,68 9,9 10,03 10,50 10,52
	n 1 = 11			n 2 = 11

Критерий Уайта определяем следующим образом. Ранжируем варианты обоих рядов по двум линиям.

хi
уi

хi
уi

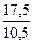
хi
уi

Каждому измерению назначаем ранг – число, соответствующее его порядковому номеру после ранжирования. Одинаковым измерениям назначаем одинаковые ранги, поровну разделяя между ними их порядковые номера.

Суммируем ранги по отдельным линиям. Сумма рангов по линии х_i:

Т _х = 2 · 6,5 + 9 + 2· 11,5 + 3 · 15 + 17,5 + 2 · 21,5 = 150,5

Сумма рангов по линии у_i:

Т_у = 2 · 1,5 + 2 · 3,5 + 5 + 2 · 9 + 13 + 17,5 + 2 · 19,5 = 102,5

Меньшая из этих сумм есть критерий Уайта. В примере Т_у = 102,5.

В дальнейшем обращаемся к таблице Уайта и при заданной надежности Р и объемах исходных выборок n ₁ и n ₂ находим значение граничного критерия Т_гр.

Для статистической достоверности сравниваемых групп рассматриваем следующие неравенства: если Т ≥ Т_гр – недостоверно; если Т < Т_гр – достоверно.

Таким образом при найденном критерии Т = 102,5 граничное значение Т_гр = 96,0 при надежности Р = 0,95 и объемах выборок n ₁ = 11 и n ₂ = 11.

Поскольку Т > Т_гр различие между сравниваемыми группами недостоверно. Следовательно, исследуемые группы баскетболистов и футболистов по становой силе различимы между собой несущественно.

Критерий знаков непараметрический, выборки большие, равновеликие, соблюдение нормального закона необязательно.

Критерий применим в случае попарного альтернативного сравнения групп. При этом возможны сравнения, обусловленные изменением признака с течением времени, или сравнения аналогичного признака в двух различных группах.

Критерий знаков предполагает исследование каких-либо показателей при оценке их изменения. Изменение прогрессивное выражается знаком «+», регрессивное знаком «–». Так при сравнении характеристик одной и той же группы с течением времени (предыдущие и последующие измерения) знак «+» назначается при улучшении показателя, знак «–» – при его ухудшении. В практике спорта под улучшением в одних случаях понимается увеличение абсолютного значения (прирост силы), в других – их уменьшение (время забега, заплыва).

Таким образом, при сравнении нескольких групп измерений назначается соответствующий знак. В дальнейшем производим оценку статистически достоверных (недостоверных) различий между совокупностями положительных и отрицательных значений. Для этого обращаемся к таблице Ван дер Вардена и при определенной надежности Р и количестве исследуемых пар n без нулевых значений n–Z(0) находим граничное значение критерия знаков Z_гр, представляющее собой интервал. При нахождении отрицательных измерений Z(–) внутри этого интервала наблюдается статистическая недостоверность между исследуемыми показателями в сравниваемых группах, в противном случае – достоверность.

Пример 4.3.5. У 32 спортсменов измерена относительная сила разгибателей ног (сила обеих ног в сумме в ньютонах на 10 кг массы спортсмена) в начале подготовительного периода х_i и в конце у_i. Установить достаточно ли эффективно изменилась относительная сила разгибателей ног у этих спортсменов в течение подготовительного периода.

В таблице 4.3.10 назначаем Z(y_i – x_i) – знаки каждой паре сравниваемых показателей. При увеличении относительной силы ставим знак «+», при уменьшении знак «–», при отсутствии изменений – «0». Из таблицы следует, что количество улучшений, ухудшений и отсутствие таковых соответственно: Z(+) = 17, Z(–) = 5, Z(0) = 10. В дальнейшем задаваясь надежностью Р = 0,95 при количестве исходных пар n = 32 без учета нулевых изменений Z(0) = 10

n₁ = n – Z(0) = 32 – 10 = 22,

из таблицы Ван дер Вандера находим Z_гр = |6…16|.

Таким образом относительная сила разгибателей ног у данных спортсменов изменилась статистически достоверно, так как Z(–) = 5 находится вне интервала Z_гр. Следовательно, по исследуемому показателю в течение подготовительного периода тренировочные занятия следует считпть эффективными.

Таблица 4. 3.10

хi	yi	Z(yi-xi)		xi	yi	Z(yi-xi)
7,20 7,30 7,40 7,50 7,90 8,10 8,20 8,30 8,40 8,50 8,60 8.90 8,90 9,00 9,10 9,10	7,20 7,35 7,45 7,60 7,80 8,00 8,30 8,35 8,50 8,50 8,65 8,90 8,95 9,10 9,15 9,10	+ + + - - + + + + + + +		9,10 9,40 9,50 9,50 9,60 9,60 9,60 9,60 9,70 9,70 9.80 9.80 9,80 9,80 9,90 9,90	9,05 9,45 9,60 9,65 9,70 9,60 9,60 9,80 9,65 9,70 9,85 9,80 9,75 9,80 10,00 9,90	- + + + + + - + - +

5. Корреляция. О взаимном влиянии признаков

В спортивных исследованиях часто требуется установить взаимное влияние процессов или явлений. Если бы такие процессы можно было выразить одним числом, то при выявлении влияния друг на друга, например, двух процессов, достаточно было бы сравнить два числа. Взаимное влияние каких-либо признаков друг на друга может выражаться различно. Влияние может быть значительным, и тогда говорят о тесной связи между такими признаками, оно может быть слабым — связь между ними очень мала и т. д. В математике существуют два принципиальных подхода к анализу тесноты связи между признаками.

Во-первых, математически можно выразить самую тесную связь между признаками — функциональную. Функциональная связь отражает такое взаимное влияние признаков, когда одному значению какого-либо признака точно соответствует одно определенное значение другого признака. Например, определенной длине стороны квадрата точно соответствует одна, единственная площадь квадрата, вес тела соответствует определенному значению его массы. В этих случаях связь между признаками совершенно точная и может быть выражена точной формулой или графиком. Такого рода связи встречаются в точных науках — физике, геометрии, механике и т. д.

Во-вторых, существуют связи, которые отражают неточное или неполное взаимное влияние. Например, общеизвестно, что между ростом и весом людей существует взаимосвязь, однако, точной ее назвать нельзя. Люди одного роста могут иметь разную массу. Исследовав людей с одной и той же температурой, находим, что частота пульса у них различна, хотя между температурой и частотой пульса есть определенная связь.

Взаимная связь между признаками, когда одному значению первого признака соответствует множество значений другого признака, называется корреляционной или статистической связью. Если такая связь велика, говорят, что признаки тесно (или сильно) коррелируют, в противном случае — признаки слабо коррелируют.

По своему характеру корреляция бывает прямой (положительной) и обратной (отрицательной).

Прямая корреляция отражает однотипность в изменении признаков: с увеличением значений первого признака увеличиваются значения и другого, или с уменьшением первого уменьшается второй.

Обратная корреляция указывает на увеличение первого признака при уменьшении второго или уменьшение первого признака при увеличении второго.

Например, больший прыжок и большее количество тренировок — прямая корреляция, уменьшение времени, затраченного на преодоление дистанции, и большее количество тренировок— обратная корреляция.

Дата добавления: 2015-10-24