Понятие о нормальном законе распределения

Ранее были рассмотрены примеры, в которых приводились разнообразные случайные явления (события). Как правило, их выражают числом. Представим себе, что один какой-нибудь вид случайного события имеет разное выражение числом. Например, надо определить вероятность того, что при определенной степени физической подготовки спортсмен сможет выполнить прыжок в высоту 160 см, затем 175 см, затем 180 см и т.д.

Прыжок в высоту 160 см – случайное событие, а несколько случайных событий, выраженных разными числами, называются случайными величинами. Значит, прыжок х = 160 см – есть случайное событие, а прыжки х ₁ =160 см; х ₂=175 см, х ₃ = 180 см и т. д. есть случайные величины.

В соответствии с определением вероятности возможно определить вероятность каждого прыжка Р(х ₁), Р(х ₂), Р(х ₃) и т. д.

Соотношение между случайными величинами и соответствующими им вероятностями называется законом распределения случайных величин.

Наиболее простой формой выражения такого закона является таблица, в которой каждому значению случайной величины соответствует вероятность ее появления. Такая таблица называется рядом распределения случайных величин (табл. 3.3.1):

Таблица 3.3.1

х 1	х 2	х 3	… …	хn
P(x 1)	P(х 2)	P(х 3)	… …	P(хn)

Пример 3.3.1. На тренировочных занятиях спортсмен выполнил 50 прыжков в высоту. Из них: 32 прыжка – 160 см; 12 прыжков – 175 см и 6 прыжков – 180 см. Вероятность того, что спортсмен на соревнованиях покажет результат

P₁(160 см)= =0,64,

где m = 32 – благоприятствующие исходы для прыжка 160 см; n = 50 – равновозможные.

Вероятность того, что спортсмен на соревнованиях покажет результат

P₂ (175 см)= =0,24,

где m = 12 – благоприятствующие исходы для прыжка 175 см; n = 50 – равновозможные.

Вероятность того, что спортсмен на соревнованиях покажет результат

P₃ (180 см)= =0,12,

где m = 6 – благоприятствующие исходы для прыжка 180 см; n = 50 – равновозможные.

Составим ряд распределения случайных величин (табл. 3.3.2):

Таблица 3.3.2

х i	160 см	175 см	180 см
Р(х i)	0,64	0,24	0,12

На основании этой таблицы данное распределение можно выразить графиком (рис. 3.3.1). Отложим на оси Х масштаб для случайных величин x _i (в одной единице длины – 5 см высоты), а на оси Y – масштаб для выражения вероятностей Р(х _i) (в единице длины – 0,1 вероятности). Нанесем на график все три пары чисел, как результат пересечения вертикалей и горизонталей из соответствующих точек. Полученные точки соединим плавной кривой – она и будет представлять собой график данного распределения.

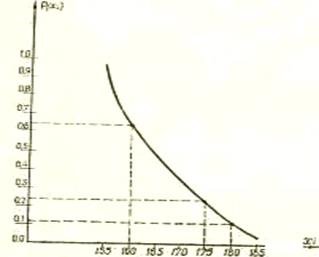
Рис. 3.3.1. Закон распределения случайных величин в примере 25

Особый интерес представляют распределения, которые имеют одинаковый график, хотя при этом рассматриваются самые разнообразные случайные величины. Такие распределения носят характер обобщающих и имеют свое выражение формулой, графиком, таблицей.

Самым распространенным среди них является нормальный закон распределения случайных величин. Его еще называют законом Гаусса по имени выдающегося немецкого математика Карла Гаусса, определившего свойства этого закона.

Внешний вид нормального закона распределения представляет собой плавную кривую, симметричную относительно средней линии (рис. 3.3.2).

Рис. 3.3.2. Нормальный закон распределения.

Среди свойств нормального закона особенно интересны такие.

1). Вершина кривой всегда точно приходится на точку , представляющую собой среднюю арифметическую всех случайных величин.

2). Высота кривой нормального закона характеризуется величиной среднего квадратического отклонения: чем больше этот фактор рассеивания, тем ниже и более плоско выглядит вершина, и чем меньше среднее квадратическое, тем острее и выше вершина.

3). Медиана и мода нормального распределения совпадают и равны средней арифметической

4). Площадь под всей этой кривой равна единице и выражает тот факт, что, пересмотрев все случайные величины и их вероятности, получаем суммарную их вероятность максимальной: Р = 1.

5). К числу замечательных свойств нормального закона относится распределение площади на участках оси х, равных ±1s, ±2s, ±3s. Знаки ± перед s возникли вследствие того, что начало оси координат можно перенести в точку – от этого общая картина графика не нарушается. В этом случае 3s, отложенные влево от начала координат, будут с минусом, а вправо – с плюсом. Оказывается, что на участке ±1s площадь под кривой составляет 0,6828 от всей площади, на участке ±2s = 0,9545, а на участке ±3s = 0,9973 от всей площади. Это позволяет нам хотя бы приблизительно ориентироваться, является ли какое-либо эмпирическое распределение нормальным. Рассмотрим это подробней (рис. 3.3.3).

Рис. 3.3.3. К правилу трех сигм.

Площадь под 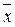±3s составляет 0,9973 от всей площади – это почти вся вероятность появления рассмотренных случайных величин,

Обратим внимание на то, что вероятность, определяемая по формуле Р(А)= , пропорциональна числу рассматриваемых случайных событий. В связи с этим можно сказать, что под кривой нормального закона на участке 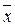±3s должно находиться 0,9973 всех случайных событий.

Это свойство нормального закона привело к одному из практических способов, позволяющему установить нормальность закона: если на участке ±3s содержится 0,9973 часть от объема совокупности, закон нормален.

Приведенное правило ±3s (читается: правило плюс-минус трех сигм) представляет собой приближенный способ проверки ряда на нормальность распределения и применяется в случае первичных прикидочных расчетов.

Большинство задач математической статистики без преувеличения имеет принципиальное решение на основе свойств нормального закона. Это относится, в частности, и к тем задачам, которые применимы в спорте.

Следует отметить, что подавляющее большинство эмпирических распределений в спорте соответствует нормальному закону. Вследствие этого нормальный закон и задачи, решаемые на основании использования его свойств, имеют огромное значение в практике спортивных исследований.

4. Репрезентативность выборочных показателей.

Генеральная совокупность – это наиболее общая совокупность объектов, объединенных каким-либо признаком.

Чтобы получить исчерпывающую информацию о состоянии той или иной статистической совокупности, нужно учесть весь ее состав без исключения. Однако, в силу разных обстоятельств, не всегда есть возможность прибегать к сплошному обследованию изучаемых совокупностей. Вследствие этого анализу подвергается какая-то их часть, по которой судят о состоянии всей совокупности в целом. Эта отобранная из генеральной совокупности часть называется выборкой.

Выборочная совокупность (или выборка) – это часть генеральной, выбранная из нее и подлежащая исследованию.

Характеристики генеральной совокупности – средняя величина, дисперсия, среднее квадратическое отклонение представляют собой величины постоянные. По отношению к ним соответствующие выборочные характеристики, которые служат оценками генеральных параметров, являются величинами случайными: они могут совпадать и не совпадать с величиной генеральных параметров. Отсюда возникает вопрос о репрезентативности выборочных показателей.

4.1. Ошибки репрезентативности.

Теоретически доказано и практически подтверждено, что если правильно и полно подобрать выборочную совокупность, она достаточно точно представляет (говорят: репрезентатирует) генеральную. Возможные отклонения выборочных показателей от их параметров в генеральной совокупности называются ошибками репрезентативности. Эти ошибки неизбежны и возникают потому, что исследованию подвергается не вся генеральная совокупность, а только ее малая доля (выборка).

Это ошибки не технические, а статистические, возникающие не в процессе измерений или учета единиц совокупности и не вследствие вычислительной работы, а исключительно в силу недостаточной точности, с какой выборка репрезентатирует генеральную совокупность. Но, как и ошибки, допускаемые при измерении, выборочные ошибки, или ошибки репрезентативности, могут быть и случайными, и систематическими. Первые возникают независимо от воли экспериментатора, вторые являются следствием несоблюдения условий репрезентативности при образовании выборочной совокупности.

Систематические ошибки снимаются с устранением вызывающих их причин, главным образом, при соблюдении принципа произвольности, который предполагает, что доброкачественная выборка должна быть объективной, т.е. производиться без предвзятых побуждений, при исключении субъективных влияний на ее состав.

Случайные же ошибки репрезентативности остаются и должны учитываться при оценке генеральных параметров по данным выборочных наблюдений. При сплошном изучении генеральной совокупности ошибки репрезентативности не имеют места.

Размеры выборочных ошибок зависят главным образом от объема выборки и от размаха варьирования значений. В частности, чем больше объем выборки, тем меньше выборочная средняя характеристика отличается от генеральной средней. Следовательно, при увеличении числа испытаний ошибка выборочной средней будет уменьшаться.

Достаточно репрезентативной по численности следует считать выборку из 30 объектов — такой объем удобен в исследовании и отвечает закону больших чисел о том, чтобы численность выборки была достаточно объемной.

Возможно, составить выборку и из 15—20 объектов, однако репрезентативность ее будет достаточной только тогда, когда члены генеральной совокупности подлежат распределению в соответствии с нормальным законом.

По-видимому, выборку менее 10 объектов нельзя считать репрезентативной.

Таким образом, численность выборочной совокупности следует принимать n=30, а если это невозможно по каким-либо обоснованным причинам, принимать n=15—20 и не менее 10. В последнем случае точность выводов снижена.

Доказательства оптимальности таких объемов связаны со свойствами нормального закона и распределения Стьюдента, имеющего своим пределом тоже нормальное распределение.

На величину средней ошибки влияет также размах варьирования признака: чем больше размах варьирования, тем больше будет и величина выборочной ошибки, при сравнительно слабом варьировании признака ошибка средней арифметической оказывается меньше.

Основная задача выборочного метода — определение средней арифметической генеральной совокупности _ген. без исследования всех объектов ее объема. Для решения такой задачи необходимо составить выборку, репрезентатирующую данную генеральную совокупность. В полученной выборке найти ее среднюю арифметическую _выб.

Установлено, что, если выборочная совокупность достаточно хорошо представляет генеральную, средняя арифметическая выборки _выб репрезентатирует среднюю арифметическую генеральной совокупности _ген. При этом, средняя выборки _выб не может быть точно равна средней генеральной совокупности _ген., а отличается от нее, так как какой бы репрезентативной не была выборка, ее объем меньше объема генеральной и, таким образом, подобный анализ не может отразить истинного существа дела. С учетом выше сказанного, чем больше объем выборочной совокупности, тем точнее выборка представляет генеральную и тем меньше должно быть различие в средних _ген и _выб. Также, говоря о характеристике средней арифметической генеральной _ген. посредством выборочной _выб., следует говорить о вероятности, с которой гарантируется определенная точность счета.

В связи с этим, в рассматриваемой задаче существуют два основных понятия: ошибка репрезентативности m и надежность Р (или еще говорят: доверительная вероятность) и ее характеристика—критерий надежности t.

4.2.Критерий надежности.

Ошибка репрезентативности указывает на величину различия между средними арифметическими генеральной и выборочной совокупностей.

Определить ошибку репрезентативности можно двумя способами.

Если выборочная совокупность составлена таким образом, что любой объект генеральной может попасть в выборку несколько раз, то ошибку репрезентативности можно определить по формуле:

(4.2.1)

где m – ошибка репрезентативности, s_выб – среднее квадратическое отклонение выборочной совокупности, n – объем выборки.

Более точной является формула:

(4.2.2)

где (n – 1) представляет собой так называемое число степеней свободы.

Число степеней свободы есть количество вариантов, принимающих произвольные значения, не меняющие величину средней арифметической.

При объемах выборки n=30 различие между n и (n—1) практически не ощущается, вследствие чего можно пользоваться любой из формул (4.2.1) или (4.2.2). При выборках численностью менее 30 такое различие более ощутимо. В этом случае предпочтительна формула (4.2.2).

Если выборка образована из генеральной таким образом, что любой объект генеральной совокупности не может быть в ней повторим, ошибка может быть определена по формуле:

(4.2.3)

где m – ошибка репрезентативности; s _выб. – среднее квадратическое отклонение выборочной совокупности; n – объем выборки; N – объем генеральной совокупности.

Очевидно, что, пользуясь формулой (4.2.3), необходимо знать численность генеральной совокупности N, без чего можно обойтись в формулах (4.2.1) и (4.2.2). Отсюда следует, что если численность генеральной совокупности неизвестна, как это часто имеет место в спортивных работах, выборочную совокупность нужно отбирать посредством первого способа и пользоваться формулами (4.2.1) и (4.2.2).

Допустим, установлена величина ошибки репрезентативности. Желательно знать не только величину абсолютного расхождения между средними арифметическими генеральной и выборочной совокупностей, но и определить точность произведенного расчета. Характеристикой такой точности является надежность.

Надежность (доверительная вероятность) есть вероятность, с которой гарантируется точность расчетов при определении генеральной средней (посредством выборочной). Поскольку число, выражающее вероятность в соответствии с определением вероятности, не выходит за пределы единицы, надежность, выраженная числом, естественно, меньшим единицы, может быть дополнена до единицы, так сказать, «оставшейся» вероятностью. Такая вероятность называется уровнем значимости b.

Например, если надежность есть Р=0,95, то дополнением до полной вероятности, равной единице, есть величина 0,05. Таким образом, уровень значимости здесь b=0,05.

В рассматриваемой задаче до начала вычислений задают надежность, необходимую для данных исследований (или задают уровень значимости). Как правило, надежность на должном уровне обеспечивается достаточным объемом выборки. Вследствие этого, надежность и объем выборочной совокупности должны быть взаимно увязаны.

Эта взаимосвязь изложена в таблице Стьюдента, где каждому значению надежности соответствует объем выборочной совокупности. Таким образом, таблица Стьюдента представляет собой информацию по определению критерия надежности и объема выборки, соответствующих определенной надежности (см. приложение 2). Будет ли она приложена?

Какой же надежностью следует пользоваться в спортивных исследованиях? Специальных указаний по этому поводу дать нельзя. Следует выбирать надежность для конкретной задачи, так же необходимо обеспечить объем выборки, соответствующий избранной надежности, пользуясь таблицей Стьюдента.

Ниже приводятся значения надежностей, принимаемых во многих исследованиях спорта. Считается достаточно высокой для точности и необременительной по объему выборки надежность р₁=0,95. Это самое распространенное значение надежности. Надежность Р₂=0,99 принимается в спорте реже. Здесь речь идет о повышенных требованиях точности. Наконец, очень редко в спорте встречается третье значение надежности Р₃=0,999. Как правило, это медицинские работы. Для этих трех надежностей объем выборки и критерии надежности находим по таблице Стьюдента (табл. 4.2.1).

Таблица 4.2.1.

Надежность	Критерии надежности	Объем выборки
Р1=0,95 Р2=0,99 Р3= 0,999	t1=2,04(»2,0) t2=2,75 t3=3.65	n1>30 n2>30 n3>30

Попутно обратим внимание на то, что численность выборки n=30, предложенная ранее, способна гарантировать нужные для расчета надежности.

Возвратимся к задаче определения средней арифметической генеральной совокупности посредством выборочной. Для определения искомой _ген, выборочный метод предлагает определить границы, называемые нижним и верхним доверительными интервалами, в пределах которых должна находиться средняя арифметическая генеральной совокупности. Формула определения _ген. выглядит так:

(4.2.4)

где _ген. — средняя арифметическая генеральной совокупности;

— нижняя доверительная граница;

— верхняя доверительная граница;

от [ 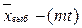] до [ ] – доверительный интервал;

– средняя арифметическая выборочной совокупности;

m – ошибка репрезентативности;

t – критерий надежности.

Иногда произведение называют абсолютной погрешностью, как некоторый общий показатель ошибки репрезентативности и надежности.

Таким образом, для определения средней арифметической генеральной совокупности, составляем выборку, исследуем ее обычным методом средних величин, находим по одной из вышеприведенных формул ошибку репрезентативности, задавшись надежностью, находим критерий надежности по таблице Стьюдента. Полученные данные подставляем в формулу (4.2.4) и находим те пределы, в которых должна находиться искомая средняя арифметическая генеральной совокупности. При помощи этого метода получим информацию о генеральной совокупности, не исследуя ее объектов, а перенося ее с определенной степенью точности с выборочной совокупности.

Отсюда следует, что при эмпирических распределениях, соответствующих нормальному закону, найденные выборочным методом величины _ген. и s_ген. могут дать весьма полное представление о всей генеральной совокупности.

Рассмотрим примеры по определению доверительных границ.

Пример 4.2.1. В школе 730 мальчиков 14 лет. Из них группа школьников в 50 человек исследована на силу ног по количеству приседаний в течение 20 с. По результату исследований этих 50 школьников можно сделать вывод о средних возможностях 730. х _i —количество приседаний за 20 с.; n _i —количество школьников, показавших данный результат.

Результаты обработаны методом средних величин в табл. 4.2.2:

Таблица 4.2.2

xi	ni	xini	xi-	(xi- )^2	(xi- )^2ni
			-4
			-3
			-2
			-1
			+1
			+2
			+3
			+4
	n=50

N=730; n=50;

В соответствии с формулой (4.2.3), т.к. известно N определяем величину ошибки репрезентативности:

Найденная ошибка m = 0,3 свидетельствует о том, что величину _ген – среднюю арифметическую количества приседаний 730 школьников – также можно принять _ген.=13,0, как и у 50 школьников _выб =13,0. Однако при этом погрешность такого предположения составит 0,3 приседания.

Зададимся надежностью P₁ = 0,95, которой по таблице Стьюдента соответствует критерий надежности t» 2,0. Находим величину (mt) – абсолютную погрешность счета: m t = 0,3·2,0» 0,6.

Нижняя доверительная граница [ _выб – (mt)] = 13,0 – 0,6 = 12,4» 12,0. Верхняя доверительная граница [ _выб. + (mt)] = 13,0 + 0.6 = 13,6» 14.0.

Таким образом, средние возможности 730 школьников находятся в пределах: 12,0 < _ген.< 14,0, то есть от 12 до 14 приседаний в течение 20 с.

Напомним здесь еще раз о некоторой академичности подобных примеров: числа здесь округляются и рассматривается небольшое их количество, практически же подлежит расчету значительно большее число вариантов.

Задача о нахождении средней арифметической генеральной совокупности по выборочной есть одна из возможных. Существуют, например, задачи, где необходимо определить доверительную вероятность и др.

Дата добавления: 2015-10-24