Задание 3. Автокорреляция случайных возмущений и гетероскедастичность

Пусть имеются следующие условные данные (X- объясняющая переменная, Y- зависимая переменная, данные выбрать по вариантам из табл. 1). Рассчитать статистику Дарбина-Уотсона. Сделать вывод о наличии гетероскедастичности.

1. Для анализа коррелированности случайных отклонений используют статистику Дарбина—Уотсона DW, рассчитываемую по формуле

.

Общая схема критерия Дарбина—Уотсона следующая:

1.1. По построенному эмпирическому уравнению регрессии

определяются значения отклонений для каждого наблюдения t, t=1, … T.

1.2. По формуле рассчитывается статистика DW.

1.3. По таблице критических точек Дарбина- Уотсона определяются два числа d_l и d_u и осуществляют выводы по правилу:

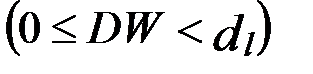- существует положительная автокорреляция,

- вывод о наличии автокорреляции не определен,

- автокорреляция отсутствует,

- вывод о наличии автокорреляции не определен,

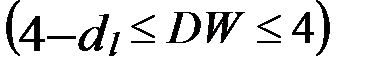- существует отрицательная автокорреляция.

Рассчитаем статистику Дарбина-Уотсона. Для этого построим вспомогательную таблицу 7:

Таблица 7

Вспомогательная таблица для расчета критерия Дарбина-Уотсона

…
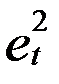
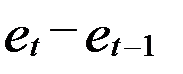
Σ					-

2. Возможным методом устранения автокорреляции остатков является итеративный процесс, называемый методом Кохрана–Оркатта. На примере парной регрессии он описывается так.

2.1. Оценивается регрессия по МНК, т.е. находится уравнение и определяются остатки .

2.2. Оценивается коэффициент авторегрессии случайных возмущений

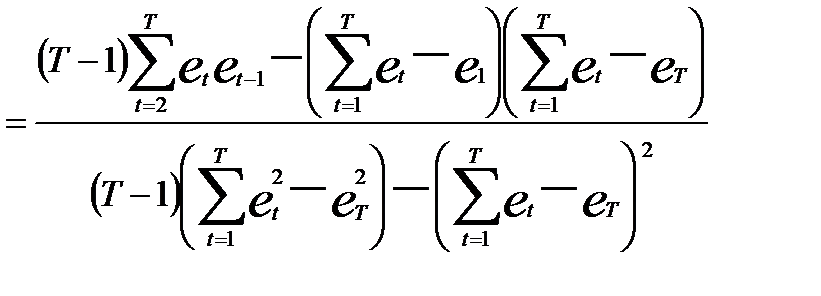
2.3. Рассчитываются «новые» значения переменных

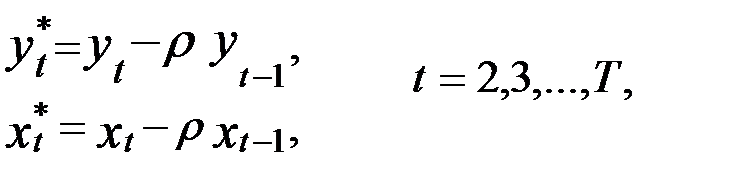
2.4. Определяются коэффициенты уравнения .

2.5. Значения подставляются в . Вновь вычисляются оценки отклонений и вновь вычисляется статистика Дарбина-Уотсона.

2.6. Если необходимо сделать прогноз на период , то применяют формулу

,

где используются параметры, полученные после последней итерации.

3. Для оценки гетероскедастичности данные необходимо выстроить в порядке возрастания объясняющей переменной x.

Уравнение регрессии, построенное по всем исходным данным, имеет вид .

Для оценки гетероскедастичности применим тест Голдфелда-Квандта.

3.1. Для этого разобьем упорядоченные данные на две группы в соотношении 5 на 5.

3.2. Уравнение регрессии, построенное по первым 5 данным, имеет вид , сумма квадратов остатков равна S₁. Уравнение регрессии, построенное по вторым 5 данным, имеет вид , сумма квадратов остатков равна S₂.

3.3. F- статистика равна F=S₁/S₂ или F=S₂/S₁ (в числителе должна быть большая сумма квадратов), что необходимо сравнить с табличными значениями при уровнях значимости 5% и степенями свободы ν=n₁-m и ν=n₂-m (где n₁ и n₂ – число наблюдений в 1 и 2 группах соответственно, m – число оцениваемых параметров в новых уравнениях регрессии).

Чем больше величина F превышает табличное значение F-критерия, тем больше нарушена предпосылка о равенстве дисперсий остаточных величин, т.е. проявляется гетероскедастичность.

Дата добавления: 2015-08-20