|
Читайте также: |
Пусть
где Y1t - объем продукции; Y2t - стоимость основных производственных фондов; X1t - поставки сырья; X2t-1 - объем инвестиций в предыдущем году;
X3t-1 - количество работающих в предыдущем году.
Данную модель можно записать в виде:
Необходимо исследовать идентифицируемость первого уравнения. Так как в него не входят переменные X2t-1 и X3t-1, матрица А1 параметров при этих переменных имеет вид:
.
Определитель равен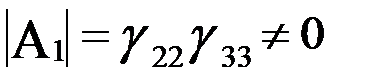 
, следовательно, ранг А1 равен 2.
Модель состоит из трех уравнений (содержит три эндогенные переменные), поэтому выполняется условие
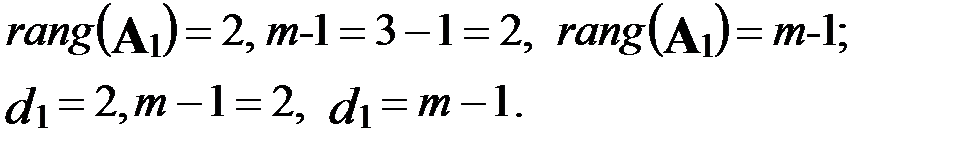
Таким образом, первое уравнение системы однозначно идентифицируемо.
Рассмотрим идентифицируемость второго уравнения. В него не входят переменные 
. Матрица А2 имеет вид:
.
Эта матрица имеет ранг равный 2, если не равен нулю хотя бы один из определителей
был отличен от нуля. Очевидно, что это условие выполняется. Второе уравнение неоднозначно идентифицируемо, так как
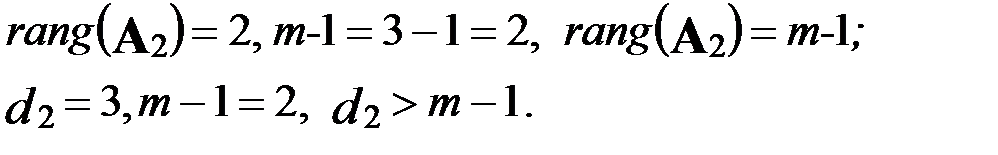
Исследуем третье уравнение. В нем отсутствуют переменные 
. Матрица А3 параметров при этих переменных имеет вид:
.
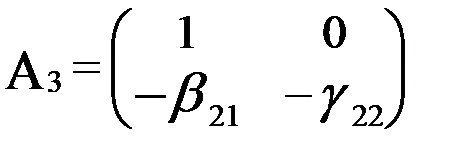Определитель равен 
, следовательно,
Третье уравнение однозначно идентифицируемо.
Таким образом, все уравнения и модель в целом идентифицируемы. Существует возможность оценить параметры модели.
Дата добавления: 2015-08-20; просмотров: 75 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание 12. Исследование взаимосвязи показателей с помощью непараметрических методов | | | Как правильно определить размер и сделать заказ? |