|
Читайте также: |
Исходные данные берем из табл.3, 4 и 5.
Для примера пусть исходные содержатся в табл. 8. Коэффициент корреляции объясняющих переменных 
, что свидетельствует о сильной мультиколлинеарности объясняющих переменных.
Таблица 8.
Данные для исследования мультиколлинеарности гребневым методом
| 
| 
|
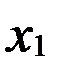
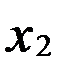
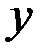
| 1,4 | ||
| 3,1 | ||
| 10,3 | ||
| 10,6 | ||
| 7,6 | ||
| 7,4 | ||
| 4,4 | ||
| 5,8 | ||
| 11,9 |
Диагональные элементы обратной матрицы 
, которые связаны со стандартными ошибками коэффициентов уравнения регрессии, равны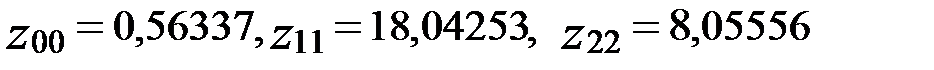 
Рассмотрим «гребневой метод» («ридж-регрессия») устранения мультиколлинеарности. Метод был предложен А. Э. Хоэрлом в 1962 году и применяется когда матрица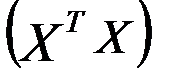 
близка к вырожденной. К диагональным элементам матрицы 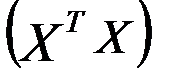добавляют некоторое небольшое число (от 0,1 до 0,4). При этом получают смещенные оценки параметров уравнения. Но стандартные ошибки таких оценок в случае мультиколлинеарности ниже ошибок даваемых обычным методом наименьших квадратов.
Прибавим 0,4 к диагональным элементам матрицы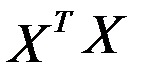 
:
Тогда получим уравнение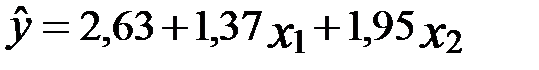 
. Диагональные элементы обратной матрицы значительно снизятся и будут равны 
, что приводит к снижению стандартных ошибок коэффициентов.
Дата добавления: 2015-08-20; просмотров: 85 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание 3. Автокорреляция случайных возмущений и гетероскедастичность | | | Задание 5. Фиктивные переменные. |