Задание 1. Парная линейная регрессия

Задания для практических работ на семинарах

Тема 1.2. Метод наименьших квадратов. Парная линейная регрессия. Анализ построенной модели.

Задание 1. Парная линейная регрессия

Для анализа зависимости объема потребления y (ден. ед.) домохозяйства от располагаемого дохода x (ден. ед.) отобрана выборка объема n = 10 домохозяйств, результаты которой приведены в таблице1.

Таблица 1.

Выборка домохозяйств зависимости объема потребления y домохозяйства от располагаемого дохода x

Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y	0,5	0,7	0,9	1,1	1,4	1,4	1,7	1,9	1,8	1,1
x
Вариант
i
y
x
Вариант
i
y
x
Вариант
i
y
x

1. Оценить тесноту связи между признаками x и y.

2. Оцените коэффициенты уравнения парной линейной регрессии по методу наименьших квадратов. Оцените на сколько единиц в среднем изменится переменная y, если переменная x вырастет на 1 единицу.

3. Проверьте статистическую значимость оценок b₀, b₁ теоретических коэффициентов β0, β1 при уровнях значимости α=0,05.

4. Сделайте вывод о качестве подобранного уравнения. Рассчитайте коэффициент детерминации. Рассчитайте t-статистику для коэффициента детерминации и оцените его статистическую значимость.

5. Рассчитайте 95%-е доверительные интервалы для теоретических коэффициентов регрессии. Спрогнозируйте значение зависимой переменной y при x_p =160 и рассчитайте 95% доверительный интервал для условного математического ожидания зависимой переменной. Рассчитайте границы интервала, в котором будет сосредоточено не менее 95% возможных значений y при x_p =160.

Для выполнения задания необходимо заполнить вспомогательную таблицу 2 (графы с 1 по 6).

Таблица 2.

Вспомогательная для расчетов уравнения регрессии

i	y	x	y^2	x^2	xy
…	…	…	…	…	…	…	…	…
…	…	…	…	…	...	…	…	…
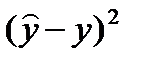
Σ

1. Для оценки тесноты связи между признаками x и y необходимо выполнить следующее:

1.1. рассчитать линейный коэффициент корреляции

1.2. Написать выводы по величине R по шкале Чэддока. Если =0 – связь отсутствует, если <0,3 – связь несущественная, если 0,3< 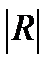<0,5 – связь слабая, если 0,5< <0,7 – связь средняя (умеренная), если 0,7< <1 – связь сильная (тесная), если =1 – связь функциональная. Если R<0 – связь обратная, если R>0 – связь прямая.

1.3. Рассчитать коэффициент алиенации

1.4. Рассчитать ошибку коэффициента корреляции

1.5. Рассчитать значимость коэффициента корреляции по t -критерию Стьюдента

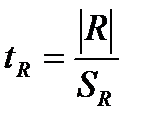
1.6. Сравнить полученное значение с табличным при уровне значимости α=0,05 (доверительной вероятности 0,95) и числе степеней свободы ν=n-2. Если t_R > t_табл, то коэффициент корреляции признается значимым и делается вывод о том, что между объемом потребления домохозяйства и изменением располагаемого дохода есть тесная статистическая взаимосвязь.

2. Для оценки коэффициентов уравнения парной линейной регрессии по методу наименьших квадратов необходимо:

2.1. Рассчитать средние значения у и х

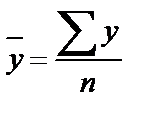
2.2. Рассчитать параметры линейного уравнения регрессии

2.3. Сделать вывод о том, что коэффициент регрессии b₁ показывает, что с увеличением располагаемого дохода на 1 ден. ед. объем потребления домохозяйства возрастает (уменьшается) на ____ ден. ед.

2.4. Рассчитать коэффициенты эластичности факторов

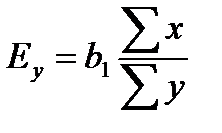
Величина коэффициента эластичности позволяет сделать вывод, что с увеличением фактора x на 1 % результативный признак увеличивается на ___ %.

2.5. Рассчитать значения

где – функция взаимосвязи между факторным признаком x и результативным признаком y, b₀ и b₁ – параметры линейного уравнения регрессии.

2.6. Подставляя в полученное уравнение регрессии значения x, можно определить условные (расчетные, теоретические) значения . Для этого заполнить графу 7 таблицы 2.

2.7. Проверить точность расчета: Σ y ≈ Σ .

3. Проверьте статистическую значимость оценок b₀, b₁ теоретических коэффициентов β₀, β₁ при уровнях значимости α =0,05.

Для этого необходимо:

3.1. Рассчитать остаточную дисперсию, заполнив графу 10 таблицы 2.

3.2. Оценить дисперсии коэффициентов b₀, b₁ , заполнив графу 9 табл.2.

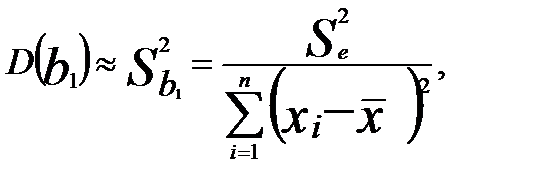
3.3. Рассмотреть проверку статистической значимости коэффициентов парной линейной регрессии. При проверке гипотезы H₀:α_j=0 против альтернативной гипотезы H₁:α_j≠0, для коэффициентов b₀ и b₁ рассчитываются абсолютные величины t-статистик коэффициентов:

.

3.4. При выполнении исходных предпосылок модели эти дроби имеют распределение Стьюдента с числом степеней свободы ν=n-2, где n - число наблюдений. Рассчитанное значение t -статистики сравнивается с критическим значением , где α - требуемый уровень значимости. В данном случае рассматривается двухсторонняя критическая область. Коэффициент полагается статистически значимым, если абсолютная величина его t -статистики превосходит .

3.5. Рассмотреть определение интервальных оценок коэффициентов линейного уравнения регрессии. Доверительные интервалы для коэффициентов имеют вид:

.

Фактически доверительный интервал определяет значения теоретических коэффициентов регрессии β₀ и β₁, которые будут приемлемыми с надежностью 1-α при найденных оценках b₀ и b₁.

4. Для проверки качества подобранного уравнения проверить значимость коэффициента детерминации:

4.1. Общее качество уравнения регрессии оценивается по тому, как хорошо эмпирическое уравнение регрессии согласуется со статистическими данными. Для принятия гипотезы об одновременном равенстве нулю всех коэффициентов линейной регрессии коэффициент детерминации R² не должен существенно отличаться от нуля. Поэтому для анализа значимости всех коэффициентов регрессии исследуют значимость коэффициента детерминации. Таким образом, коэффициент детерминации R² является суммарной мерой общего качества уравнения регрессии, он рассчитывается по формуле (заполнив графу 8 табл. 2):

4.2. Коэффициент детерминации определяет долю разброса зависимой переменной, объяснимую регрессией y на x. В общем случае справедливо соотношение . Чем теснее линейная связь между y и x, тем ближе коэффициент детерминации R² к единице. Чем слабее такая связь, тем R² ближе к нулю. С помощью коэффициента детерминации R² и сделать вывод о том, на сколько процентов изменение объема потребления y домохозяйства объясняется изменением располагаемого дохода x.

4.3. Проверить гипотезу о статистической значимости коэффициента детерминации R²: H₀: R²=0 против альтернативной гипотезы H₁: R²>0. Для проверки данной гипотезы часто используется следующая F-статистика:

,

где n - число наблюдений, m - число объясняющих переменных (т.е. 1). В случае парной линейной регрессии . Величина F при выполнении предпосылок МНК и при справедливости H₀ имеет распределение Фишера. Показатели F и R² равны или не равны нулю одновременно. Для проверки нулевой гипотезы H₀: F=0, R²=0 при заданном уровне значимости α по таблицам критических точек распределения Фишера находится критическое значение . Нулевая гипотеза отклоняется, если . Это равносильно тому, что R²>0, т.е. R² статистически значим.

5. Для расчета 95%-е доверительных интервалов для теоретических коэффициентов регрессии необходимо:

5.1. Рассмотреть определение доверительных интервалов для зависимой переменной. Сначала рассмотреть предсказание среднего значения (математического ожидания) зависимой переменной. С заданной надежностью 1-α при любом конкретном значении x объясняющей переменной доверительный интервал для имеет вид:

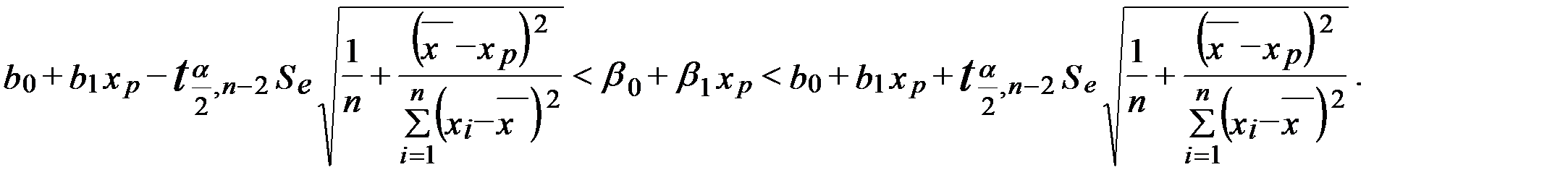
5.2. Рассмотреть предсказание индивидуальных значений зависимой переменной. Пусть нас интересует некоторое возможное значение y₀ переменной Y при определенном значении x_p объясняющей переменной X. Тогда интервал

определяет границы, за пределами которых могут оказаться не более 100α% точек наблюдений значений Y при X=x_p. Построенные интервалы наиболее узкими будут при 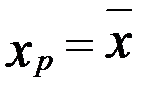. По мере удаления x_p от среднего значения доверительные интервалы расширяются. Поэтому необходимо достаточно осторожно экстраполировать полученные результаты на прогнозные области. С другой стороны, с ростом числа наблюдений эти интервалы сужаются к линии регрессии.

Дата добавления: 2015-08-20