Задание 12. Исследование взаимосвязи показателей с помощью непараметрических методов

Студент выбирает свой вариант (из приведенных выше таблиц 3, 4 и 5) и делает расчет показателей.

1. Заполнить вспомогательную таблицу 20

Таблица 20

Вспомогательная таблица расчета коэффициента конкордации

n	y	x1	x2	Rx1	Rx2	Ry	ΣRx1x2y	(ΣRx1x2y)^2
…	…	…	…	…	…	…	…	…
…	…	…	…	…	…	…	…	…
Σ	–	–		–	–	–	Σ=H	Σ=G

2. Рассчитать коэффициент конкордации и его значимость

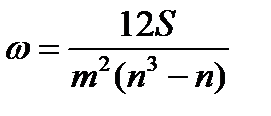
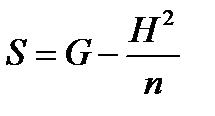
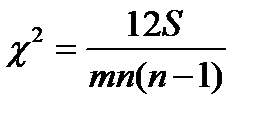
где G– сумма квадратов сумм рангов, H– сумма рангов, m– количество изучаемых явлений, n– количество признаков явления.

3. Если при числе степеней свободы (df= n– 1) и значимости α =0,05, расчетный критерий χ ² больше табличного, то коэффициент конкордации считается значимым.

4. Заполнить вспомогательную таблицу 21

Таблица 21

Вспомогательная таблица расчета коэффициента Фехнера

n	y	x1	x2	знаки	С	Н	знаки	С	Н
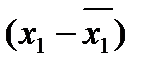
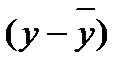
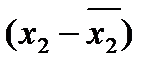
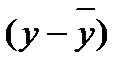
Σ	–	–		–	–			–	–

5. Рассчитать коэффициент корреляции знаков Фехнера для показателя у и двух показателей х.

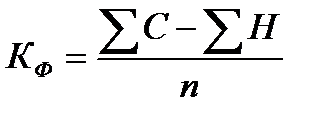
где ∑С – совпадения знаков отклонений от средних значений x и y, ∑Н – несовпадения знаков отклонений.

6. Определить значимость коэффициента корреляции знаков. Если 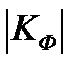=0 – связь отсутствует, если 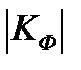<0,3 – связь несущественная, если 0,3< 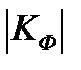<0,5 – связь слабая, если 0,5< 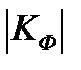<0,7 – связь средняя (умеренная), если 0,7< 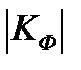<1 – связь сильная (тесная), если 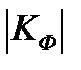=1 – связь функциональная. Если K_Ф<0 – связь обратная, если K_Ф >0 – связь прямая.

7. Определить наибольший показатель для признака х (по модулю). Заполнить вспомогательную таблицу 22, причем показатели х расположить по возрастанию

Таблица 22

Вспомогательная таблица расчета коэффициентов корреляции рангов

n	y	x	Rx	Ry	d^2	Q	P
Σ	–	–	–	–

8. Рассчитать коэффициент корреляции рангов Спирмэна между y и выбранным x

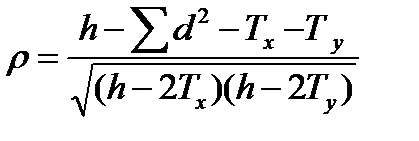
где

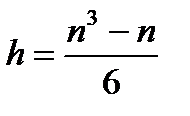
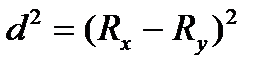
R_x и R_y – ранги значений x и y.

T_x и T_y – ранговые поправки

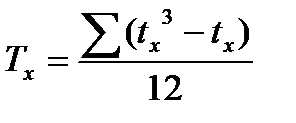
где t_x t_y –количество связных рангов в группе

9. Определить значимость коэффициента корреляции по таблице 23

Таблица 23

Значимость коэффициента корреляции рангов Спирмэна

n
ρтабл	0,900	0,829	0,745	0,714	0,683	0,636	0,609	0,580	0,555
n
ρтабл	0,534	0,518	0,500	0,485	0,472	0,458	0,445	0,435	0,424
n
ρтабл	0,415	0,406	0,398	0,389	0,382	0,375	0,369	0,362

Если ρ > ρ_табл при уровне значимости α=0,05- коэффициент корреляции значимый, связь существенна.

Если 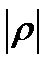=0 – связь отсутствует, если 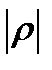<0,3 – связь несущественная, если 0,3< 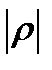<0,5 – связь слабая, если 0,5< 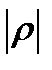<0,7 – связь средняя (умеренная), если 0,7< 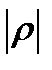<1 – связь сильная (тесная), если 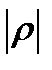=1 – связь функциональная. Если ρ <0 – связь обратная, если ρ >0 – связь прямая.

10. Рассчитать коэффициент корреляции рангов Кендалла между y и x

где 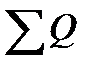- число случаев, когда у последующих значений у ранг больше, чем у данного, 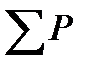- число случаев, когда у последующих значений у ранг меньше, чем у данного.

11. Определить значимость коэффициента корреляции рангов. Если 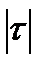=0 – связь отсутствует, если 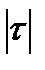<0,3 – связь несущественная, если 0,3< 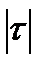<0,5 – связь слабая, если 0,5< 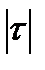<0,7 – связь средняя (умеренная), если 0,7< 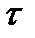<1 – связь сильная (тесная), если 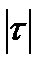=1 – связь функциональная. Если τ <0 – связь обратная, если τ >0 – связь прямая.

12. Сгруппировать страны по двум признакам в 2 группы (до среднего значения и более среднего значения), построить вспомогательную таблицу 24 («четырех полей»)

Таблица 24

Вспомогательная таблица расчета критерия "хи-квадрат"

		1 признак	Сумма
Менее среднего	Более среднего
2 признак	Меньше среднего	…	a	…	b	…
Больше среднего	…	c	…	d	…
Сумма	…	…	…

13. Рассчитать коэффициенты ассоциации и контингенции

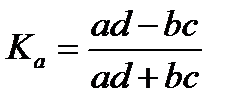
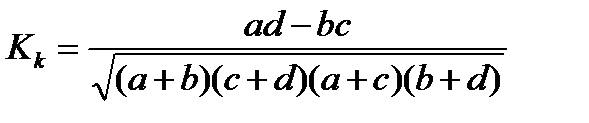
14. Сделать вывод, если |K_a|>0,5, |K_k|>0,3, то существует связь между явлениями.

15. Рассчитать критерий χ² и φ²

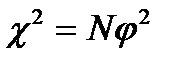
N= a+ b+ c+ d

ν= (n₁ – 1)(n₂ – 1)

16. Если при числе степеней свободы ν и значимости α =0,05, расчетный критерий χ ² меньше табличного, то гипотеза об отсутсвии влияния одного фактора на другой не опровергается.

17. Рассчитать коэффициенты взаимной сопряженности Пирсона и Чупрова

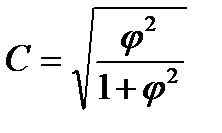
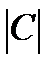18. Написать выводы по величине коэффициентов взаимной сопряженности Пирсона и Чупрова по шкале Чэддока. Если =0 – связь отсутствует, если <0,3 – связь несущественная, если 0,3< 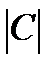<0,5 – связь слабая, если 0,5< 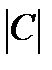<0,7 – связь средняя (умеренная), если 0,7< <1 – связь сильная (тесная), если 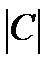=1 – связь функциональная. Аналогично по величине K.

---

Дата добавления: 2015-08-20