Читайте также:
|
Квадратичной функцией называется функция вида
Координаты вершины параболы
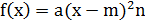
Свойства квадратичных функций:
1) Область определения R
2) Множества значений
При a>0 промежуток 
.
При a<0 промежуток 
.
3) График функций пересекает ось абсцисс при D≥0 в точках с абсциссами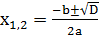 
;приD<0парабола не имеет общих точек с осью абсцисс. Это точки называются нулями функции.
4) Функция ы точке 
a<0и наименьшее значения при a>0,равное 
Дата добавления: 2015-08-17; просмотров: 53 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Показательные неравенства | | | Рациональная функция |