|
Читайте также: |
1) Еслиa>1, тоaf(x)>ag(x)→f(x)>g(x)
2) Если0<a<1, то af(x)>ag(x)→f(x)<g(x)
3) af(x) >c, a>0, a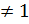 
;
a) c>0, 0<a<1, тоf(x)<logac
b) c>0,a>1,тоf(x)>logac
c) c≤0 тоxϵR
4) af(x)>c, a>0, a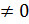 
;
a) c>0, 0<a<1, то f(x)>logac
b) c>0, a>1, то f(x)<logac
c) c≤0, то решений нет.
5) 
то
и 
6) 
то
и 
Логарифмические неравенства a>0, a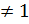
| a>1 | |
| logaf(x) > k | 
| 
|
| logaf(x) ≤ b | f(x)≥ab |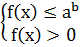 
|
| logaf(x) >logag(x) | 
| 
|
| logaf(x) ≤ logag(x) |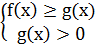 
| 
|
logf(x)g(x)>logf(x)h(x)равносильно совокупности систем
и 
Logf(x)g(x)≤logf(x)h(x) равносильно совокупности систем
и 
Дата добавления: 2015-08-17; просмотров: 57 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тригонометрические неравенства | | | Квадратичная функция |