Логарифмические уравнения

Log_af(x)=log_ag(x)→f(x),a>0,a≠1;

Виды:

1. Log_af(x)=b→f(x)=a^b;

2. Log_af(x)+ Log_ag(x)= Log_ah(x)↔f(x)g(x)=h(x)

3. →P(y)=0;

4. Log_h(x)f(x)=b→

5. Log_k(x)f(x)=log_k(x)g(x)→

Неравенства

Линейные неравенства

ax<b→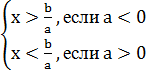

Квадратные неравенства

ax²+bx+c>0,a>0→

ax²+bx+c 0,a>0→

ax²+bx+c<0,a>0→

ax²+bx+c≤0,a>0→

Неравенства с переменной под знаком модуля

|f(x)|*|g(x)|↔f²(x)*g²(x), где *∈(>,<,≥,≤)

|f(x)|>g(x)↔

|f(x)|<g(x)↔

Дата добавления: 2015-08-17