Тригонометрические неравенства

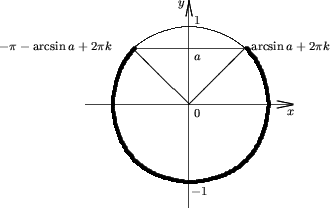
Функция синуса:

1) Множества решений неравенства: 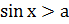есть

1.R, еслиa<-1;

2. если-1≤a<1;

(arcsin a + 2 k; π- arcsin a +2 k);

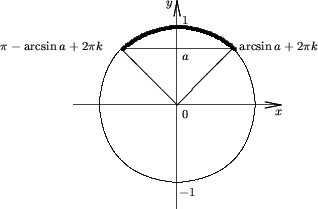3.пустое множество, еслиa≥1

2) Множества решений неравенства sinx<a есть

1. R, еслиa ≥1;

2. Если -1 <a ≤ 1,

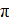(- - arcsina + 2 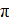k; arcsina + 2 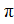k); -1 <a ≤ 1;

3. Пустое множество, еслиa ≤ -1

Функция косинуса:

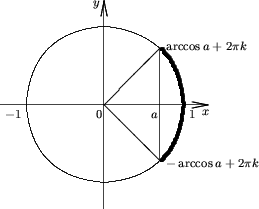
2) Множества решений неравенства: cosx>aесть

1. R, если a< -1;

(2 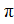k - arccosa; 2 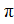k + arccosa);

если-1 ≤ a< 1;

2. Пустое множество, еслиa ≥ 1

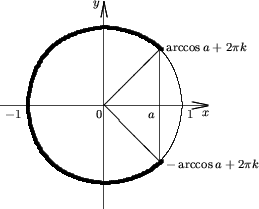
1) 2) Множества решений неравенстваcosx<aесть

1. R,еслиa> 1;

2. (2 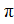k + arccosa; 2 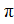(k + 1) - arccosa),если-1 <a ≤ 1;

3. Пустое множество, если a ≤ -1

Функция тангенса:

2) Множества решений неравенства: tgx>aесть

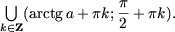
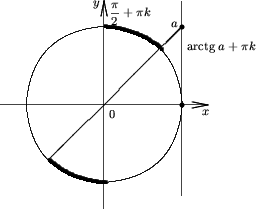
3) Множества решений неравенства: tgx<aесть

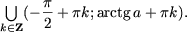
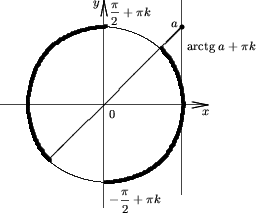
Функция котангенса:

1) Множества решений неравенства: ctgx>a есть

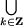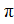( k; arcctga + 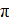k).

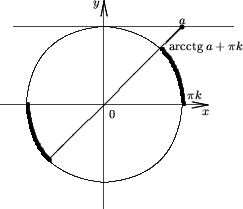
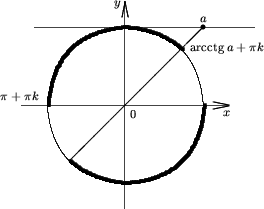
2) Множества решений неравенства: ctgx<aесть

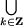(arcctga + 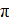k; 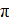(k + 1))

Дата добавления: 2015-08-17