Промежутки возрастания и убывания заданной функции

Пусть функция y = f(x) непрерывна, определена и дифференцируема на промежутке Х и равенство 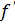(х)=0 выполняется для конечных чисел точек данного промежутка.

1) Решение неравенства показывает промежуток возрастания функции.

2) Решение неравенства показывает промежуток убывания функции.

Наибольшее и наименьшее значения непрерывной функцией y = f(x) в промежутке [a;b]:

1) Находится .

2) Находим критическое точки решая уравнение .

3) Выясняем, принадлежит ли полученные критические точки промежутку [a;b].

4) Находим значения функции y = f(x) на концах отрезка [a;b]

5) Сравнивая полученные значения функции, определяем наибольшее и неименьшее значения.

Дата добавления: 2015-08-17