|
Читайте также: |
Рассмотрим простейший и самый распространенный случай, когда 
- многочлен. Требуется построить многочлен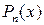 
степени 
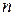, который в заданных точках 
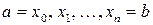(узлах интерполирования) принимает заданные значения 
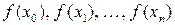. Легко доказать, что такой многочлен только один. При помощи простых выкладок можно построить интерполяционный многочлен вида [5]
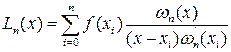, (7.10.1)
где
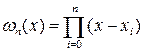. (7.10.2.)
Интерполяционный полином (7.10.1) называют интерполяционным полиномом Лагранжа.
Дата добавления: 2015-08-03; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача интерполирования | | | Погрешность интерполирования |